Radicale di radicale
Ciao a tutti, stavo facendo degli esercizi quando in un risultato finale mi son imbattuto in questo: $ sqrt(2sqrt(6) ) xy $.
Io avrei lasciato il risultato scritto in questo modo ma esso risulta scomponibile in questa maniera: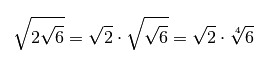
Quello che non capisco è come si giunga a tale risultato. Io banalmente avrei provato ad applicare la regola "radice di radice" (anche se il 2 in mezzo reca fastidio) e sarebbe venuto come risultato \( 2\sqrt[4]{6} \)
Ho provato a scrivere il radicale in SymboLab e dà questo suggerimento:

ma nemmeno qui lo capisco, c'è qualcosa che mi sfugge!
Supponendo tutto il radicale sia \( \sqrt[n]{ab} \) e supponendo che \( \sqrt[n]{a} \) = \( \sqrt[]{2} \) ed \( \sqrt[n]{b} \) = \( \sqrt[4]{6} \) , applicando la regola non dovrebbe venire \( \sqrt[]{2} \sqrt[4]{6} \) ? Dunque, da dove sbuca quel doppio radicale? Qual è il passaggio che proprio non colgo?
*Prima di postare definitivamente ho avuto un flash: forse ho sbagliato a definire i termini. E se fosse \( a = \sqrt{1} \) e se \( b = 2\sqrt[4]{6} \) allora \( \sqrt{1}\sqrt{2\sqrt[4]{6}} \) ???
E' comunque diversa la posizione del 2...
Vi ringrazio per la pazienza!
Io avrei lasciato il risultato scritto in questo modo ma esso risulta scomponibile in questa maniera:
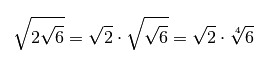
Quello che non capisco è come si giunga a tale risultato. Io banalmente avrei provato ad applicare la regola "radice di radice" (anche se il 2 in mezzo reca fastidio) e sarebbe venuto come risultato \( 2\sqrt[4]{6} \)

Ho provato a scrivere il radicale in SymboLab e dà questo suggerimento:

ma nemmeno qui lo capisco, c'è qualcosa che mi sfugge!

Supponendo tutto il radicale sia \( \sqrt[n]{ab} \) e supponendo che \( \sqrt[n]{a} \) = \( \sqrt[]{2} \) ed \( \sqrt[n]{b} \) = \( \sqrt[4]{6} \) , applicando la regola non dovrebbe venire \( \sqrt[]{2} \sqrt[4]{6} \) ? Dunque, da dove sbuca quel doppio radicale? Qual è il passaggio che proprio non colgo?

*Prima di postare definitivamente ho avuto un flash: forse ho sbagliato a definire i termini. E se fosse \( a = \sqrt{1} \) e se \( b = 2\sqrt[4]{6} \) allora \( \sqrt{1}\sqrt{2\sqrt[4]{6}} \) ???
E' comunque diversa la posizione del 2...
Vi ringrazio per la pazienza!
Risposte
Non ho capito molto delle tue elucubrazioni ma quest'espressione $sqrt(2sqrt(6))$ non è altro che questa $sqrt(2*sqrt(6))$ e quindi si può applicare la proprietà $root(n)(ab)=root(n)(a)*root(n)(b)$
Hai ragione, mea culpa per quanto riguarda la chiarezza 
Fin qui ci sono, se \( \sqrt[n]{ab} \) = \( \sqrt{2.\:\sqrt{6}} \) allora \( a = \sqrt{2} \) e \( b = \sqrt{6} \)
moltiplicando viene \( \sqrt[2]{12} \). Dove sbaglio?

Fin qui ci sono, se \( \sqrt[n]{ab} \) = \( \sqrt{2.\:\sqrt{6}} \) allora \( a = \sqrt{2} \) e \( b = \sqrt{6} \)
moltiplicando viene \( \sqrt[2]{12} \). Dove sbaglio?
Eh, no ...
Sotto la radice "grande" (quella più esterna) ci sta il prodotto $2*sqrt(6)$ cioè $a=2$ e $b=sqrt(6)$
Sotto la radice "grande" (quella più esterna) ci sta il prodotto $2*sqrt(6)$ cioè $a=2$ e $b=sqrt(6)$
Troppe ore di studio portano a questi risultati, alla fine non capisci più niente. 
Stamattina l'ho ripreso ed effettivamente era molto semplice, ti ringrazio per l'aiuto!
Stamattina l'ho ripreso ed effettivamente era molto semplice, ti ringrazio per l'aiuto!


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo