Problemi moto armonico e moto relativo (trasformazioni galileiane)
Ciao a tutti, oggi il solito prof. pazzo di fisica ci ha dato 6 problemi da risolvere (da consegnare domani!). Quelli sul moto armonico li ho capiti e dovrei averli risolti correttamente. Invece non ho capito niente di niente sul moto relativo e le trasformazioni di Galileo: fosse stata una lezione sulla traduzione dall'antico aramaico ci avrei capito di più. I problemi sono:
1)Una molla disposta orizzontalmente, alla cui estremità è vincolato un punto materiale P, oscilla con frequenza $3 Hz$. Sapendo che l'accelerazione massima in modulo vale $|amax|=5m/s^2$, calcola il modulo della velocità massima $|vmax|$ del punto P.
2)Un punto materiale P si muove di moto armonico con ampiezza $A=20 cm$ e frequenza $f = 2 Hz$. Sapendo che all'istante iniziale $t=0$ il punto si trova nella posizione $x0=A$, calcola la posizione, la velocità e l'accelerazione a $t=3 s$.
3)Enuncia il principio di relatività galileiano e scrivi le leggi di trasformazione (vettoriale) delle posizioni e delle velocità in relatività galileiana.
4)Un'auto A si muove rispetto al suolo con velocità $vA=90 (km)/h$ e incrocia una seconda auto B che si muove in direzione opposta con velocità $v'B=220 (km)/h$ rispetto ad A. Calcola la velocità B rispetto al suolo.
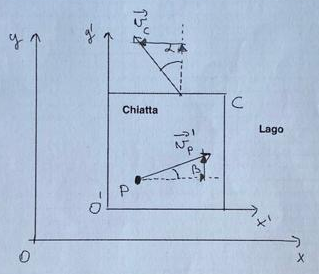
5)Una chiatta C si sta muovendo su un lago, la cui acqua è in quiete rispetto alla riva, con una velocità in modulo uguale a $|vc|=8 m/s$ e diretta come in figura. Sulla chiatta una persona P sta camminando con una velocità in modulo uguale a $|vP|=2 m/s$ e diretta come in figura. Si consideri $α=30°$ e $β=20°$. Calcolare la velocità $vP$ della persona rispetto alla riva.
Figura disegnata a mano dal prof.:
6)In autostrada, un tir B supera un tir A. Sapendo che la lunghezza del tir A è $lA=15 m$ e la lunghezza del tir B è $lB=18 m$ e che rispetto al suolo $vA=75 (km)/h$ e $vB=90 (km)/h$, calcola il tempo (minimo) che il tir B deve trascorrere in corsia di sorpasso.
I primi due sul moto armonico li ho risolti così:
1)$ω=2πf$ ----> $ω=6,28*3=18,84 rad/s$. Poichè $amax=A*ω^2$ ---> $A=amax/ω^2=5/354,94=0,014m$ . A questo punto trovo $vmax=ω*A=18,84*0,014=0,26 m/s$
2)$A=20 cm= 0,2 m$. Poichè $ω=2πf$ ----> $ω=6,28*2=12,56 rad/s$. Poiche $x(t)=Acos(ωt)$ trovo la posizione al tempo t=3 s ----> $x(3s)=0,2*cos(12,56*3)=0,2*0,79=0,15 m$. La velocità a t = 3 s è $v=-Aω*sin(ωt)$ -----> $v=-0,2*12,56*sin(12,56*3)=-2,51*0,61=-1,53 m/s$. L'accelerazione è $a=-Aω^2*cos(ωt)=-0,2*157,75*0,79=-24,92 m/s^2$.
3)Sul libro ho trovato questo principio:
Per le formule: $x'=x-vt$, $y'=y$, $z'=z$, $t'=t$ ma non so se siano quelle giuste.
Mi potete aiutare con i problemi 4-5-6? Non so neanche da che parte cominciare.
1)Una molla disposta orizzontalmente, alla cui estremità è vincolato un punto materiale P, oscilla con frequenza $3 Hz$. Sapendo che l'accelerazione massima in modulo vale $|amax|=5m/s^2$, calcola il modulo della velocità massima $|vmax|$ del punto P.
2)Un punto materiale P si muove di moto armonico con ampiezza $A=20 cm$ e frequenza $f = 2 Hz$. Sapendo che all'istante iniziale $t=0$ il punto si trova nella posizione $x0=A$, calcola la posizione, la velocità e l'accelerazione a $t=3 s$.
3)Enuncia il principio di relatività galileiano e scrivi le leggi di trasformazione (vettoriale) delle posizioni e delle velocità in relatività galileiana.
4)Un'auto A si muove rispetto al suolo con velocità $vA=90 (km)/h$ e incrocia una seconda auto B che si muove in direzione opposta con velocità $v'B=220 (km)/h$ rispetto ad A. Calcola la velocità B rispetto al suolo.
5)Una chiatta C si sta muovendo su un lago, la cui acqua è in quiete rispetto alla riva, con una velocità in modulo uguale a $|vc|=8 m/s$ e diretta come in figura. Sulla chiatta una persona P sta camminando con una velocità in modulo uguale a $|vP|=2 m/s$ e diretta come in figura. Si consideri $α=30°$ e $β=20°$. Calcolare la velocità $vP$ della persona rispetto alla riva.
Figura disegnata a mano dal prof.:

6)In autostrada, un tir B supera un tir A. Sapendo che la lunghezza del tir A è $lA=15 m$ e la lunghezza del tir B è $lB=18 m$ e che rispetto al suolo $vA=75 (km)/h$ e $vB=90 (km)/h$, calcola il tempo (minimo) che il tir B deve trascorrere in corsia di sorpasso.
I primi due sul moto armonico li ho risolti così:
1)$ω=2πf$ ----> $ω=6,28*3=18,84 rad/s$. Poichè $amax=A*ω^2$ ---> $A=amax/ω^2=5/354,94=0,014m$ . A questo punto trovo $vmax=ω*A=18,84*0,014=0,26 m/s$
2)$A=20 cm= 0,2 m$. Poichè $ω=2πf$ ----> $ω=6,28*2=12,56 rad/s$. Poiche $x(t)=Acos(ωt)$ trovo la posizione al tempo t=3 s ----> $x(3s)=0,2*cos(12,56*3)=0,2*0,79=0,15 m$. La velocità a t = 3 s è $v=-Aω*sin(ωt)$ -----> $v=-0,2*12,56*sin(12,56*3)=-2,51*0,61=-1,53 m/s$. L'accelerazione è $a=-Aω^2*cos(ωt)=-0,2*157,75*0,79=-24,92 m/s^2$.
3)Sul libro ho trovato questo principio:
"I fenomeni meccanici si svolgono nello stesso modo in tutti i sistemi di riferimento inerziali".
Per le formule: $x'=x-vt$, $y'=y$, $z'=z$, $t'=t$ ma non so se siano quelle giuste.
Mi potete aiutare con i problemi 4-5-6? Non so neanche da che parte cominciare.
Risposte
Veramente non sai da che parte cominciare?
Per esempio, l'auto $A$ del 4) si vede arrivare incontro un'altra auto a $220\text(km/h)$; dato che $A$ sta andando a $90\text(km/h)$ l'altra auto andrà a $130\text(km/h)$. Finito.
Per esempio, l'auto $A$ del 4) si vede arrivare incontro un'altra auto a $220\text(km/h)$; dato che $A$ sta andando a $90\text(km/h)$ l'altra auto andrà a $130\text(km/h)$. Finito.
Ah è così banale? In realtà ci avevo pensato ad una cosa del genere ma temevo di dire una castroneria...anche il numero 5 ha una soluzione così semplice? 
Ti sembra che vadano nella stessa direzione barca e persona? Usa la regola del parallelogramma per trovare la risultante della somma delle due velocità (due vettori).
Anche il 6) è semplice: il veicolo $B$ va a $15\text(km/h)$ rispetto ad $A$ quindi quanto tempo impiegherà a percorrere $15+18=33\text( m)$ ?
Anche il 6) è semplice: il veicolo $B$ va a $15\text(km/h)$ rispetto ad $A$ quindi quanto tempo impiegherà a percorrere $15+18=33\text( m)$ ?
quindi nel problema 6 dovrei applicare la formula $x=vt$ ---->$t=x/v$? Prima però trasformo tutto in m/s ----> $(75)/(3,6)=20,83 m/s$ e $(90)/(3,6)=25 m/s$. A questo punto faccio $t=(33)/(25)=1,32 s$. è corretto?
Perché $25$ ? ](/datas/uploads/forum/emoji/eusa_wall.gif)
E poi, ti pare che in poco più di un secondo riesca a superarlo e sopravanzarlo di $18\text( m)$ ?
](/datas/uploads/forum/emoji/eusa_wall.gif)
E poi, ti pare che in poco più di un secondo riesca a superarlo e sopravanzarlo di $18\text( m)$ ?
credo di aver capito devo usare come velocità i $15 (km)/h$ ----> $(15)/(3,6)=4,16 m/s$ ----> $t=(33)/(4,16)=7,93 s$


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo