Problema sulla circonferenza
La circonferenza della figura ha raggio 10, la corda AB dista 6 dal centro e la retta su cui si trova Q è tangente in B alla circonferenza. Trova x in modo che $ {\bar{BP}^2+\bar{BQ}^2} / {\bar{OP}^2} <=1 $
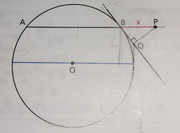
Ho iniziato a svolgere poi mi sono arenata, non riuscendo a trovare $\bar{BQ}$:
$\bar{BP}^2=x^2 $ da dati
$\bar{AB}=2*sqrt(10^2-6^
2)=16$
$\bar{OP}^2=6^2+(8+x)^2=36+64+x^2+16x=x^2+80x+36$
Su $\bar{BQ}$ mi sono bloccata... qualche aiutino?

Ho iniziato a svolgere poi mi sono arenata, non riuscendo a trovare $\bar{BQ}$:
$\bar{BP}^2=x^2 $ da dati
$\bar{AB}=2*sqrt(10^2-6^
2)=16$
$\bar{OP}^2=6^2+(8+x)^2=36+64+x^2+16x=x^2+80x+36$
Su $\bar{BQ}$ mi sono bloccata... qualche aiutino?
Risposte
.
"sellacollesella":
[quote="kyoko"]$\bar{OP}^2=6^2+(8+x)^2=36+64+x^2+16x=x^2+80x+36$
Rivedi l'ultimo passaggio.[/quote]
ops
"sellacollesella":
Indicando con \(H\) il piede dell'altezza \(BH\), ragionerei sui triangoli rettangoli \(OBH\) e \(BPQ\).
Non ci crederai ma ci ho ragionato su, e pure tanto, ma a forza di scarbocchiare non mi era venuto in mente che i due triangoli sono simili e così via... perfetto ho risolto... avendo trovato BQ ho imposto la disequazione e il risultato è giusto, grazie mille davvero
.
ciao, scusami ma sto uscendo di testa perchè non riesco proprio a trovare bq, potrei avere qualche dritta?
Se H è il piede della proiezione di B sul diametro, i triangoli OBH e BQP sono simili perchè gli angoli $hat(OBH)$ e $hat(PBQ)$ sono entrambi complementari di $hat(HBQ)$. Del primo conosci tutti i lati, del secondo conosci l'ipotenusa $x$. Imposta la proporzione, stai attenta all'ordine dei cateti.



 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo