Problema logica volume cono
Ciao a tutti,
nel seguire un percorso di letture mi sono
ritrovato a ragionare sulla dimostrazione della
formula per il calcolo del volume di un cono.
Girovagando su Google non ho trovato risposte e
ho deciso di chiedere aiuto alla vostra comunità.
Premesso che non ho una grande competenza in geometria,
mi è parso comunque utile (anche altri forse hanno di questi dubbi)
porre il quesito seguente:
se è vero, come effetivamente è vero, che la formula per il calcolo
del volume di un cono si ottiene moltiplicando l'area della sua base
per l'altezza e dividendo per tre, per quale ragione invece non si ottiene
un risultato corretto moltiplicando l'area del triangolo rettangolo
(apotema-raggio-altezza) per la circonferenza del cerchio di base ??
So che a tanti questo mio dubbio apparirà troppo elementare,
però, credo, che una buona risposta possa aiutare la divulgazione.
Grazie mille a chi vorrà rispondere
nel seguire un percorso di letture mi sono
ritrovato a ragionare sulla dimostrazione della
formula per il calcolo del volume di un cono.
Girovagando su Google non ho trovato risposte e
ho deciso di chiedere aiuto alla vostra comunità.
Premesso che non ho una grande competenza in geometria,
mi è parso comunque utile (anche altri forse hanno di questi dubbi)
porre il quesito seguente:
se è vero, come effetivamente è vero, che la formula per il calcolo
del volume di un cono si ottiene moltiplicando l'area della sua base
per l'altezza e dividendo per tre, per quale ragione invece non si ottiene
un risultato corretto moltiplicando l'area del triangolo rettangolo
(apotema-raggio-altezza) per la circonferenza del cerchio di base ??
So che a tanti questo mio dubbio apparirà troppo elementare,
però, credo, che una buona risposta possa aiutare la divulgazione.
Grazie mille a chi vorrà rispondere
Risposte
Ma non funziona così.
Non siamo noi che dobbiamo dimostrare che il tuo metodo è sbagliato (cosa che, incidentalmente, è semplice:dato che abbiamo già una formula buona, basta far vedere che la tua porta a risultati diversi) : sei tu che devi dimostrare che è giusto (come dicono i giuristi: onus probandi incumbit ei qui adfirmat)
(come dicono i giuristi: onus probandi incumbit ei qui adfirmat)
Non siamo noi che dobbiamo dimostrare che il tuo metodo è sbagliato (cosa che, incidentalmente, è semplice:dato che abbiamo già una formula buona, basta far vedere che la tua porta a risultati diversi) : sei tu che devi dimostrare che è giusto
Comunque la formula di abbidubbi è quella per il volume di un cuneo dal profilo triangolare; prova a immaginare come trasformarlo in un cono 
Lungi da me l'idea di pretendere da Voi una dimostrazione.
Nel mio caso la questione è più terra terra.
Non essendo, come in premessa, competenete in geometria
pensavo solo che qualcuno potesse rispondermi, a parte
la validità della formula nota, con qualcosa del tipo:
"... hai detto una sciocchezza perchè la rotazione del
triangolo ovviamente...etc etc "
Grazie comunque per il tempo che mi hai dedicato
Nel mio caso la questione è più terra terra.
Non essendo, come in premessa, competenete in geometria
pensavo solo che qualcuno potesse rispondermi, a parte
la validità della formula nota, con qualcosa del tipo:
"... hai detto una sciocchezza perchè la rotazione del
triangolo ovviamente...etc etc "
Grazie comunque per il tempo che mi hai dedicato
"axpgn":
Comunque la formula di abbidubbi è quella per il volume di un cuneo dal profilo triangolare; prova a immaginare come trasformarlo in un cono
Ma .. se la rotazione del triangolo sull'asse dell'altezza del cono (raggio-apotema-altezza) è completa a 360 gradi
la figura risultante non è un cono ??
"abbidubbi":
Ma .. se la rotazione del triangolo sull'asse dell'altezza del cono (raggio-apotema-altezza) è completa a 360 gradi
la figura risultante non è un cono ??
infatti... e quindi ipotizzando di farlo ruotare attorno all'asse delle x così come in figura
(cliccami per ingrandirmi)
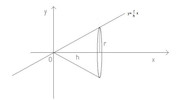
ottieni subito
$Vol_("Cono")=piint_(0)^(h)(r/h x)^2dx=pi r^2/h^2[x^3/3]_0^h=(pi r^2xxh)/3$
...che è proprio la nota formula ottenuta esattamente dal tuo ragionamento...
avevo già visto la formula con l'integrale ed è ... perfetta sotto tutti i punti di vista.
Nell'intervallo da zero a ad h sommo le infinitesime "sfoglie" del cono fino ad avere
il valore completo, che è la terza parte del volume del cilindro.
Sebbene avessi dato il titolo di "problema logica volume cono" è evidente che non
sono riuscito a spiegarmi bene. Ci riprovo!!
Siamo tutti daccordo sul fatto che il volume del cilindro è dato dalla progressiva
"sovrapposizione", nell'intervalo da zero ad h, delle infinitesime "sfoglie"
di pigreco per raggio al quadrato.
Ora mi chiedo, ma per il cono... se calcolo l'area del triangolo (raggio-apotema-altezza) e,
facendo ruotare questo triangolo di 360 gradi, vado ad aggiungere progressivamente le
infinitesime "sfoglie" di area del triangolo suddetto, ossia tante aree tanto quanto è lunga
la circonferenza di base del cono, ottengo un volume che è quello di un cuneo ma ...
non dovrebbe essere altresi vero che questo equivale anche al volume del cono ???
Nell'intervallo da zero a ad h sommo le infinitesime "sfoglie" del cono fino ad avere
il valore completo, che è la terza parte del volume del cilindro.
Sebbene avessi dato il titolo di "problema logica volume cono" è evidente che non
sono riuscito a spiegarmi bene. Ci riprovo!!
Siamo tutti daccordo sul fatto che il volume del cilindro è dato dalla progressiva
"sovrapposizione", nell'intervalo da zero ad h, delle infinitesime "sfoglie"
di pigreco per raggio al quadrato.
Ora mi chiedo, ma per il cono... se calcolo l'area del triangolo (raggio-apotema-altezza) e,
facendo ruotare questo triangolo di 360 gradi, vado ad aggiungere progressivamente le
infinitesime "sfoglie" di area del triangolo suddetto, ossia tante aree tanto quanto è lunga
la circonferenza di base del cono, ottengo un volume che è quello di un cuneo ma ...
non dovrebbe essere altresi vero che questo equivale anche al volume del cono ???
No, non dovrebbe.
Quando parli del cilindro sovrapponi i cerchi come se fossero delle "sfoglie", con il cono, invece, passi ai triangoli, invece dovresti fare riferimenti a cerchi di raggio variabile. Il problema è nel fatto che il raggio sia variabile e non costante.
Quando parli del cilindro sovrapponi i cerchi come se fossero delle "sfoglie", con il cono, invece, passi ai triangoli, invece dovresti fare riferimenti a cerchi di raggio variabile. Il problema è nel fatto che il raggio sia variabile e non costante.
"@melia":
No, non dovrebbe.
Quando parli del cilindro sovrapponi i cerchi come se fossero delle "sfoglie", con il cono, invece, passi ai triangoli, invece dovresti fare riferimenti a cerchi di raggio variabile. Il problema è nel fatto che il raggio sia variabile e non costante.
Buongiorno @melia,
nel cercare di restare in uno stretto ambito di logica, nello specifico campo concettuale del calcolo infinitesimale,
il fatto che si prendano "sfoglie" di cono nell'intervallo da zero ad h, a prescindere dal fatto che il raggio sia variabile (questo è irrilevante nell'algoritmo di integrazione), non è concettualmente diverso dal fatto che si prendano "sfoglie" di triangolo (di area definita e fissa) e le si sommi, o si calcoli l'integrale se preferisci, nell'intervallo definito dalla lunghezza della circonferenza del cerchio di base del cono.
Considera che questo sopra è il ragionamento teorico, perchè la formula che funziona, quella verificata, è
pigreco per raggio al quadrato per altezza diviso tre.
L'aiuto che cercavo, da profano in geometria, è perchè non funziona l'integrazione lungo l'intervallo della linea curva dellla circonferenza, diversamente da quella operante sul segmento dell'intervallo da zero ad h.
Prova a fare la cosa artigianalmente: riesci a costruire un cilindro sovrapponendo dei fogli circolari tutti con lo stesso diametro. Per avere un cono devi sovrapporre fogli circolari a raggio decrescente. Non puoi ottenere un cono sovrapponendo triangoli rettangoli. Non puoi pensare che sovrapporre triangoli rettangoli o farli ruotare sia la stessa cosa. Per trovare il volume di un solido di rotazione si usano gli integrali nella nota formula $V= int_a^b pi*[f(x)]^2* dx$, che poi non è altro che la somma di tutti i volumetti ottenuti dalle aree dei cerchi $pi*[f(x)]^2$ moltiplicata per la loro altezza infinitesima $dx$.
"@melia":
Prova a fare la cosa artigianalmente: riesci a costruire un cilindro sovrapponendo dei fogli circolari tutti con lo stesso diametro. Per avere un cono devi sovrapporre fogli circolari a raggio decrescente. Non puoi ottenere un cono sovrapponendo triangoli rettangoli. Non puoi pensare che sovrapporre triangoli rettangoli o farli ruotare sia la stessa cosa. Per trovare il volume di un solido di rotazione si usano gli integrali nella nota formula $V= int_a^b pi*[f(x)]^2* dx$, che poi non è altro che la somma di tutti i volumetti ottenuti dalle aree dei cerchi $pi*[f(x)]^2$ moltiplicata per la loro altezza infinitesima $dx$.
ma certo che sovrapponendo triangoli non posso ottenere un cono, ottengo un cuneo
ma io non intendevo sovrapporre le aree dei triangoli, bensì, in quanto solido di rotazione, pensavo di
ruotare appunto lungo l'altezza del cono (e quindi affiancare sommando) le tante sfoglie di area del triangolo "apotema raggio altezza". In questo modo ottengo un cono.
L'inghippo che MI vorrei sciogliere è perchè il ragionamento non funziona quando, invece di moltiplicare per l'altezza infinitesima $dx$ del cono, provo a moltiplicare la somma di tutti i volumetti delle aree dei triangoli suddetti per la lunghezza della circonferenza infinitesima $dx$ del cerchio di base.
E allora dove sta il problema? Se li sommi ottieni un cuneo, se vuoi farli ruotare non puoi sommarli.
"@melia":
E allora dove sta il problema? Se li sommi ottieni un cuneo, se vuoi farli ruotare non puoi sommarli.
Ma scusa ... la rotazione di una figura piana nello spazio è o non è la somma delle aree di detta figura
nell'intervallo in gradi da zero fino al massimo di 360 gradi ??
No. 
"axpgn":
No.
Acc...
potresti indicarmi qualche riferimento sul come
disinnescare questo mio corto circuito tra la
geometria piana e quella dei solidi ???
Non saprei, @melia è sicuramente più ferrata di me in merito 
Io posso solo farti notare che nel procedimento usato da @melia, ella non somma delle aree (cerchi) ma dei volumi ovvero dischi che hanno uno spessore sicuramente infinitesimo ma NON nullo e soprattutto costante mentre nel tuo caso quale sarebbe la dimensione non nulla, infinitesima e costante?
Io posso solo farti notare che nel procedimento usato da @melia, ella non somma delle aree (cerchi) ma dei volumi ovvero dischi che hanno uno spessore sicuramente infinitesimo ma NON nullo e soprattutto costante mentre nel tuo caso quale sarebbe la dimensione non nulla, infinitesima e costante?
Grazie per la tua risposta, mi è stata davvero utile.
E, se non ti rubo tanto tempo, vorrei dirti il perchè.
Pur essendo convinto della validità e corretteza della formula canonica provavo a fare
il calcolo del volume di un cono equilatero sia con la formula nota che con il procedimento
descritto in precedenza. Giungendo sempre ad un volume totale che in realtà era l'equivalente
di un cilindro di altezza uguale a quella del cono. Così dividendo per tre ottenvo il volume del cono.
Dopo la tua osservazione ho capito che in questo mio strambo procedimento ottenevo "roba" in più
rispetto alla figura del cono: il volume che calcolavo era quello di un cuneo avente per cateto minore
il raggio del cono, cateto maggiore la sua altezza e per ipotenusa l'apotema.
Il volume di questo cuneo equivale a quello del cilindro di raggio ed altezza simili a quelle del cono.
Come dicevi tu, "...nel tuo caso quale sarebbe la dimensione non nulla, infinitesima e costante?", in
effetti mancava un passaggio nel ragionamento.
Perchè con il ragionamento bislacco mi trovavo sempre a dover dividere per tre ??
L'errore concettuale consisteva nel trascurare il fatto che nella formula canonica, mediante l'integrale,
non si sommano "sfoglie piatte" ma "dischi volumetrici" (di spessore infinitesimo ma non nullo).
Quindi, se invece di sommare "aree piatte" di triangoli (raggio-apotema-altezza), provo a sommare
volumi di piramidi oblique a base triangolare, dove l'altezza del cono è il cateto maggiore, il raggio del cono
è il cateto minore e la terza dimensione è data dalle porzioni infinitesime della circonferenza del cerchio di base del cono, ossia dall'angolo $ alpha $ la cui ampiezza è $ lim_(alpha -> 0) $ , allora i conti tornano.
In questo modo risolvo anche il problema finale del " diviso 3" che non riuscivo a capire.
Infatti in questo modo porto "naturalmente" il tre dentro il calcolo del volume della piramide.
Chiedo scusa a tutti se non trascrivo la formula ma mi sto incasinando nella complilazione.
p.s. - per tutti coloro che son troppo seri chiedo di avere pazienza e prendere tutto ciò come gioco estivo

E, se non ti rubo tanto tempo, vorrei dirti il perchè.
Pur essendo convinto della validità e corretteza della formula canonica provavo a fare
il calcolo del volume di un cono equilatero sia con la formula nota che con il procedimento
descritto in precedenza. Giungendo sempre ad un volume totale che in realtà era l'equivalente
di un cilindro di altezza uguale a quella del cono. Così dividendo per tre ottenvo il volume del cono.
Dopo la tua osservazione ho capito che in questo mio strambo procedimento ottenevo "roba" in più
rispetto alla figura del cono: il volume che calcolavo era quello di un cuneo avente per cateto minore
il raggio del cono, cateto maggiore la sua altezza e per ipotenusa l'apotema.
Il volume di questo cuneo equivale a quello del cilindro di raggio ed altezza simili a quelle del cono.
Come dicevi tu, "...nel tuo caso quale sarebbe la dimensione non nulla, infinitesima e costante?", in
effetti mancava un passaggio nel ragionamento.
Perchè con il ragionamento bislacco mi trovavo sempre a dover dividere per tre ??
L'errore concettuale consisteva nel trascurare il fatto che nella formula canonica, mediante l'integrale,
non si sommano "sfoglie piatte" ma "dischi volumetrici" (di spessore infinitesimo ma non nullo).
Quindi, se invece di sommare "aree piatte" di triangoli (raggio-apotema-altezza), provo a sommare
volumi di piramidi oblique a base triangolare, dove l'altezza del cono è il cateto maggiore, il raggio del cono
è il cateto minore e la terza dimensione è data dalle porzioni infinitesime della circonferenza del cerchio di base del cono, ossia dall'angolo $ alpha $ la cui ampiezza è $ lim_(alpha -> 0) $ , allora i conti tornano.
In questo modo risolvo anche il problema finale del " diviso 3" che non riuscivo a capire.
Infatti in questo modo porto "naturalmente" il tre dentro il calcolo del volume della piramide.
Chiedo scusa a tutti se non trascrivo la formula ma mi sto incasinando nella complilazione.
p.s. - per tutti coloro che son troppo seri chiedo di avere pazienza e prendere tutto ciò come gioco estivo
C'è solo un inghippo nel tuo ragionamento: hai spostato il problema del "tre" dal cono alla piramide, adesso devi dimostrare perché per ottenere il volume della piramide devi dividere per tre 
Si scherza, eh ...

Si scherza, eh ...
"axpgn":
C'è solo un inghippo nel tuo ragionamento: hai spostato il problema del "tre" dal cono alla piramide, adesso devi dimostrare perché per ottenere il volume della piramide devi dividere per tre
Si scherza, eh ...
Bonn ... ma questo è più facile !!
Visto che è la formula classica e nota (non bislacca),
per il calcolo del volume di una piramide a includerlo
nel calcolo:
area del triangolo di base per l'altezza
e poi il ...diviso tre
Grazie per la tua pazienza
Ciao,
sei ancora interessato all'argomento?
sei ancora interessato all'argomento?
"nico1959":
sei ancora interessato all'argomento?
Ho qualche dubbio perché l'ultima visita dell'utente abbidubbi risale al 31/08/2019 - se clicchi sul suo nickname puoi vederlo.
Però mai dire mai... più che altro siamo al limite del necroposting.


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo