Problema di geometria sulle disuguaglianze nei triangoli

[iolanda.disimone]

Il problema è questo:
Nella figura qui sotto, è noto per ipotesi che $\alpha < \beta$ e $\delta < \gamma$. Dimostra che $AB > CD$

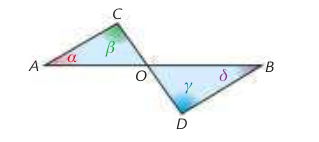
Anche qui, la teoria non so come applicarla per arrivare alla soluzione! Ho provato a impostare che l'angolo rimanente in $ACO$, che ho chiamato $\epsilon$, è uguale al suo opposto rispetto ad $O$ in quanto, appunto, opposti al vertice. Dal disegno si vede che $O$ è punto medio, ma come lo dimostro? Mi sono fermata qui e non riesco ad andare oltre. Vi chiedo gentilmente un aiuto. Grazie mille.

[@melia]

Sei sicura che $ \gamma < \delta $? E non il viceversa?

[iolanda.disimone]

"@melia":Sei sicura che $ \gamma < \delta $? E non il viceversa?

Hai ragione, ho scritto male, errore mio. Corretto.
Seguendo il ragionamento dell'altro esercizio, ho scritto che essendo $\alpha<\beta$ avrò $CO Ma come li metto in relazione tra loro? Non so come dimostrare che O è punto medio, il che mi risolverebbe tutto perché porrei $CO=OD$ e $AO=OB$

[@melia]

Non è detto che sia il punto medio, quello che importa è che C, O, D sono allineati e così pure A, O, B.

da $ CO
proprio per il fatto che sono allineati, $CD

Cita

Segnala

[iolanda.disimone]

Perfetto, tutto chiarissimo, grazie mille!