Parabola con asse non parallelo agli assi cartesiani
Salve a tutti, ho un problema nell'ottenere l'equazione di una parabola con asse di simmetria non parallelo agli assi cartesiani.
Scrivi l'equazione della parabola dato il fuoco \( F=(3;2)\text{}\) e la direttrice \( d: x-2y-9=0\text{}\).
I procedimenti che ho compiuto sono questi, ma non so come continuare. (P punto generico appartenente alla parabola e D la proiezione di tale punto sulla direttrice)
\( PD = PF\text{}\)
\( \sqrt{(x_P-x_F)^2+(y_P-y_F)^2} = \sqrt{(y_P-y_D)^2+(x_D-x_P)^2}\text{}\)
\( -6x_P+13-4y_P=-2y_Dy_P+y_D^2+x_D^2-2x_Dx_P\text{}\)
Grazie mille in anticipo
Scrivi l'equazione della parabola dato il fuoco \( F=(3;2)\text{}\) e la direttrice \( d: x-2y-9=0\text{}\).
I procedimenti che ho compiuto sono questi, ma non so come continuare. (P punto generico appartenente alla parabola e D la proiezione di tale punto sulla direttrice)
\( PD = PF\text{}\)
\( \sqrt{(x_P-x_F)^2+(y_P-y_F)^2} = \sqrt{(y_P-y_D)^2+(x_D-x_P)^2}\text{}\)
\( -6x_P+13-4y_P=-2y_Dy_P+y_D^2+x_D^2-2x_Dx_P\text{}\)
Grazie mille in anticipo
Risposte
Ciao, l'idea era giusta!
Sia $P(x, y)$ un punto della parabola. La distanza di $P$ dalla retta $d$ è $|x-2y-9|/(sqrt5)$, che va uguagliata alla distanza $\bar{PF} = sqrt((x-3)^2 + (y-2)^2)$.
Sviluppi (elevando al quadrato) e ottieni la tua parabola, cioè $4x^2+y^2+4xy-56y-12x-16=0$.
Ti torna?
PS. Posto il grafico per maggior chiarezza:
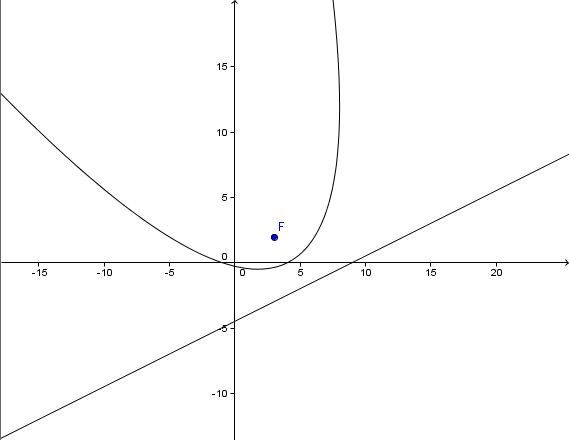
Sia $P(x, y)$ un punto della parabola. La distanza di $P$ dalla retta $d$ è $|x-2y-9|/(sqrt5)$, che va uguagliata alla distanza $\bar{PF} = sqrt((x-3)^2 + (y-2)^2)$.
Sviluppi (elevando al quadrato) e ottieni la tua parabola, cioè $4x^2+y^2+4xy-56y-12x-16=0$.
Ti torna?
PS. Posto il grafico per maggior chiarezza:

Perfetto!!!! 
Non so perchè non ho pensato subito alla distanza di un punto da una retta.
Thank you so much
Non so perchè non ho pensato subito alla distanza di un punto da una retta.
Thank you so much
"Cubrick":
Perfetto!!!!
Non so perchè non ho pensato subito alla distanza di un punto da una retta.
Thank you so much
Figurati! Per altri dubbi siamo qui


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo