Inversa di una funzione
Buongiorno, è da parecchio tempo che mi chiedo come posso invertire
$f(x)=(x-2)^2$ in $(2;+\infty)$
Avete qualche idea?
Grazie mille, a presto.
$f(x)=(x-2)^2$ in $(2;+\infty)$
Avete qualche idea?
Grazie mille, a presto.
Risposte
Per invertire una funzione sul grafico basta tracciare il suo simmetrico rispetto alla bisettrice del I e III quadrante cioè $y=x$.
Per trovare l'espressione analitica dell'inversa, invece, bisogna scambiare la $x$ con la $y$ e viceversa e esplicitare la $y$, quindi nel tuo caso diventa: $x=(y-2)^2$, $sqrt(x)=y-2$, $y=sqrt(x)+2$
Per trovare l'espressione analitica dell'inversa, invece, bisogna scambiare la $x$ con la $y$ e viceversa e esplicitare la $y$, quindi nel tuo caso diventa: $x=(y-2)^2$, $sqrt(x)=y-2$, $y=sqrt(x)+2$
Grazie, se invece avessi nella forma generale $y=ax^2+bx+c$?
A presto.
A presto.
"Fregior":
Grazie, se invece avessi nella forma generale $y=ax^2+bx+c$?
Qui si deve fare attenzione poichè in generale questa funzione non è biunivoca, quindi sarà invertibile solo a tratti, ad esempio "parte destra della parabola".
Sì, l'avevo sottinteso. Ma come si può ottenere la formula dell'inversa? (Dall'ascissa del vertice verso più infinito, ad esempio).
Grazie.
Grazie.
Scambiando le variabili ed esplicitando la $y$.
Esempio: $y=x^2+2x+1 rarr x=y^2 + 2y + 1 rarr ... rarr y=-1 +- sqrt(x)$. A seconda della scelta del segno otterrai l'inversa di una delle due parti della parabola. Posto il grafico per maggiore chiarezza:
Esempio: $y=x^2+2x+1 rarr x=y^2 + 2y + 1 rarr ... rarr y=-1 +- sqrt(x)$. A seconda della scelta del segno otterrai l'inversa di una delle due parti della parabola. Posto il grafico per maggiore chiarezza:
Però in questo caso era semplice perché avevamo $x=(y+1)^2$ se avessimo avuto, ad esempio, $y=sqrt(2)x^2+\pix+13$?
Grazie.
Grazie.
Il procedimento è lo stesso ma si complicheranno i calcoli! Nel tuo caso veniva
$y=(-pi +- sqrt(pi^2-52sqrt2+4sqrt2 x))/(2sqrt2)$. Posto il grafico nel caso del $+$.
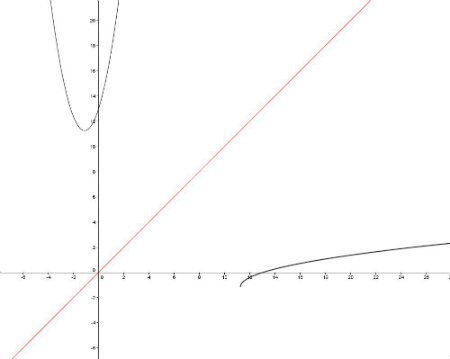
$y=(-pi +- sqrt(pi^2-52sqrt2+4sqrt2 x))/(2sqrt2)$. Posto il grafico nel caso del $+$.
"minomic":
Il procedimento è lo stesso ma si complicheranno i calcoli! Nel tuo caso veniva
$y=(-pi +- sqrt(pi^2-52sqrt2+4sqrt2 x))/(2sqrt2)$. Posto il grafico nel caso del $+$.
Il $4sqrt2 x$ da dove esce, che non ho ben capito?
Ma in pratica si fa la formula risolutiva delle equazioni di secondo grado?
Grazie.
"Fregior":
[quote="minomic"]Il procedimento è lo stesso ma si complicheranno i calcoli! Nel tuo caso veniva
$y=(-pi +- sqrt(pi^2-52sqrt2+4sqrt2 x))/(2sqrt2)$. Posto il grafico nel caso del $+$.
Il $4sqrt2 x$ da dove esce, che non ho ben capito?
Ma in pratica si fa la formula risolutiva delle equazioni di secondo grado?
Grazie.[/quote]
Eh sì! Ti trovi con $sqrt2 y^2 + pi y + 13 - x = 0$ e devi ricavare la $y$, quindi la risolvi come un'equazione di secondo grado (con $(13-x)$ da trattare come termine noto).
Tutto chiaro. Grazie tante.
"Fregior":
Tutto chiaro. Grazie tante.
Di niente!
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo