Dubbi infiniti

[dRyW]

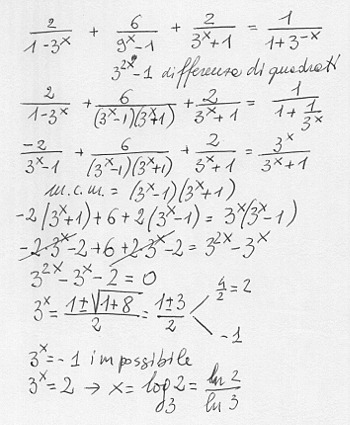
tra il secondo e terzo passaggio al secondo menbro, come fa $frac(1)(1+1/3^x)$ a diventare $frac(3^x)(3^x+1)$?

altro esercizio:

$log_e(x)=log_(10)(x)$

Svolgimento:


facendo un cambio di base,ottieniamo
$lnx=(lnx)/(ln(10))$ da cui, portando tutto a primo termine e
facendo il denominatore comune
$[(ln(10)*lnx)-lnx]/ln(10)=0$ il denominatore si può eliminare
(in quanto è diverso da 0), e rimane
$(ln(10)*lnx)-lnx=0$
ora, raccogliendo a fattor comune si ha
$lnx*(ln(10)-1)=0$
adesso abbiamo un prodotto uguale a $0$; il secondo fattore è sicuramente
un numero diverso da $0$,
per cui $lnx$ deve necessariamente essere uguale a $0$:
Pertanto $x=e^0=1$

per cambiare la base mi sembra sia questa la formula: $log_a(C)=log_a(b)*log_b(C)$

ma poi $log_e=ln$?

Per adesso mi fermo qui..grazie!

[Gi81]

Non potevi scrivere solo le tue due richieste?
1) $1/(1+1/3^x)=1/[(3^x+1)/3^x]=3^x/(3^x+1)$ (questo perchè $1/[(a/b)]=b/a$ )
2) sì, con $ln$ si indica il logaritmo in base $e$. significa "logaritmo naturale"

[chiaraotta1]

"dRyW":
...
tra il secondo e terzo passaggio al secondo menbro, come fa $frac(1)(1+1/3^x)$ a diventare $frac(3^x)(3^x+1)$?
....

$frac(1)(1+1/3^x)=frac(3^x*1)(3^x(1+1/3^x))=frac(3^x)(3^x+1)$

[dRyW]

Identità: $log_(ab) m=frac{log_a m * log_b m}{log_a m+log_b m}$

Dimostrare che vale la seguente proprietà
$log_(ab) m=frac{log_a m * log_b m}{log_a m+log_b m}$
con $a,b,m$ tali da garantire l'esistenza del logaritmo e della frazione.



Ricordiamo innanzitutto due importanti proprietà dei logaritmi:
La prima è sicuramente nota:
$logx+logy=log(xy)$ (1) per qualsiasi base positiva diversa da $1$

La seconda dice che
$log_x y=1/(log_y x)$ (2)
ovvero: un logaritmo in base $x$ di $y$ è uguale al reciproco del logaritmo con argomento e base scambiati di posto.



Iniziamo la dimostrazione sfruttando la prima proprietà (1) citata inserendo i nostri valori $a,b,m$
$log_m ab=log_m a+log_m b$

Usando ora la seconda proprietà (2)possiamo scrivere
$1/(log_(ab) m)=1/(log_a m)+1/(log_b m)$

Sommiamo le frazioni al secondo membro
$1/(log_(ab) m)=(log_a m+log_b m)/(log_a m*log_b m)$

Ora passiamo ai reciproci (se queste due frazioni sono uguali, anche i loro reciproci devono esserlo)
$log_(ab) m=(log_a m*log_b m)/(log_a m+log_b m)$

Questa era la tesi che si richiedeva, pertanto la dimostrazione, partita da una relazione sicuramente vera (la (1)) è conclusa.

probabilmente non ho completamente afferrato lo scopo di questa dimostrazione, possibilemente quello che chiederò risulterà ovvio ma abbiate pazienza..

partendo dal basso va benissimo, sono daccordo, poi però compare questa formula $log_m ab=log_m a+log_m b$

e non riesco a capire che c'entri, per me la dimostrazione si può concludere negli ultimi tre passaggi.

Mi sono pure chiesto ma se quando si vuole effettuare un cambio da base 'a' a base 'b', che succede se l'argomento coincide con base 'b'? Questo per cercare di giustificare la formula sopracitata, ma ripeto forse mi sfugge qualcosa in tutto questo

[dRyW]

up?

[dRyW]

attendendo risposta per la precedente domanda...continuo con i dubbi..



Il fatto che la base sia compresa fra 0 e 1 implica il cambio di segno?

Come mai i valori assunti dalla x sono esterni?



anche qui vi è un cambiamento di segno per quanto riguarda la terza disequazione, secondo passaggio. Non capisco nenache perchè spunta 1, $log_(1/4) (1)=0$ no?

Grazie