Coefficiente angolare
Coefficiente angolare in un punto di questa curva
x^2 + y^2 -2x -2y=0
Come si fa a calcolare il coefficiente angolare con la derivata prima?
x^2 + y^2 -2x -2y=0
Come si fa a calcolare il coefficiente angolare con la derivata prima?
Risposte
Questa è una funzione in due variabili... dapprima osservi che questa circonferenza è rappresentabile come:
$(x-1)^2 + (y-1)^2 = 2$
chiamo $X=x-1$ e $Y=y-1$ e riscrivo:
$X^2+Y^2 = 2$
ricavo $Y$:
$Y= +- sqrt(2-X^2)$
e dunque ho le due funzioni:
$Y_1 = sqrt(2-X^2)$
$Y_2= - sqrt(2-X^2)$
ovvero:
$y_1 = 1+sqrt(2-(x-1)^2)$
$y_2 = 1-sqrt(2-(x-1)^2)$
e da qui calcolo la derivata:
$Dy_1 = -X/(sqrt(2-X^2)) = -(x-1)/sqrt(2-(x-1)^2)$
$Dy_2 =X/(sqrt(2-X^2))=*(x-1)/sqrt(2-(x-1)^2)$
Chiaro?
Mod: mi ero dimenticato di una semplificazione.
$(x-1)^2 + (y-1)^2 = 2$
chiamo $X=x-1$ e $Y=y-1$ e riscrivo:
$X^2+Y^2 = 2$
ricavo $Y$:
$Y= +- sqrt(2-X^2)$
e dunque ho le due funzioni:
$Y_1 = sqrt(2-X^2)$
$Y_2= - sqrt(2-X^2)$
ovvero:
$y_1 = 1+sqrt(2-(x-1)^2)$
$y_2 = 1-sqrt(2-(x-1)^2)$
e da qui calcolo la derivata:
$Dy_1 = -X/(sqrt(2-X^2)) = -(x-1)/sqrt(2-(x-1)^2)$
$Dy_2 =X/(sqrt(2-X^2))=*(x-1)/sqrt(2-(x-1)^2)$
Chiaro?
Mod: mi ero dimenticato di una semplificazione.
Io mi ricordavo questo.. aggiungo che sapevo il punto della della tangente.
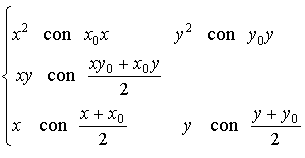
Si puo applicare a tutte le equazioni ???
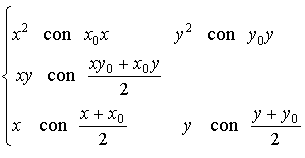
Si puo applicare a tutte le equazioni ???
"antonio0290":
Si puo applicare a tutte le equazioni ???
A tutte le coniche (parabole, circonferenze, ellissi ed iperboli)


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo