PER FAVORE NON RIESCO A FARLO
L'ALTEZZA E IL LATO OBLIQUO DI UN TRAPEZIO ISOSCELE MISURANO 12 E 15 CM. SAPENDO CHE LA DIAGONALE è PERPENDICOLARE AL LATO OBLIQUO, CALCOLA IL PERIMETRO E L'AREA DEL TRAPEZIO
Risposte
Possediamo le misure di altezza e lato obliquo, rispettivamente 12 e 15 cm. Inoltre, sappiamo che la diagonale del trapezio è perpendicolare al lato obliquo. Ti posto l'immagine di un trapezio isoscele, in modo da poterti spiegare meglio i vari procedimenti.
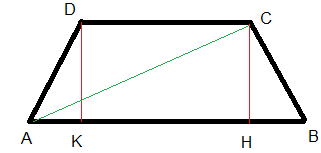
Osserviamo attentamente la figura. Il testo ci dice che AC è perpendicolare al lato obliquo (per esempio CB). Cosa significa? Che il punto d'insersezione tra CB e la diagonale genera quella condizione per la quale il triangolo ABC è rettangolo, poiché l'angolo stesso in C è retto. Per quanto concerne una delle due misure che conosciamo, CH, essa non corrisponde ad altro che all'altezza relativa all'ipotenusa del triangolo ABC. E poiché noi conosciamo quest'ultima e il lato obliquo CB (uno dei due cateti del medesimo triangolo), possiamo calcolare la misura dell'ipotenusa, che in questo caso equivale alla misura della base maggiore AB. Su questo punto arriveremo tra poco. Concentriamoci ora sul triangolo CHB. Di esso conosciamo cateto (CH) e CB (ipotenusa). Possiamo, mediante l'applicazione del teorema di Pitagora, calcolare HB, l'altro cateto:
Ora, riprendendo il punto che ho lasciato in sospeso, riconsideriamo il triangolo ABC: abbiamo bisogno di applicare il secondo teorema di Euclide (che ti consiglio vivamente di ripassare), il quale afferma che "In un triangolo rettangolo, il quadrato costruito sull’altezza relativa all’ipotenusa è equivalente al rettangolo che ha per dimensioni le proiezioni dei cateti sull’ipotenusa."
Di questi dati, noi ne conosciamo due, pertanto dobbiamo svolgere la formula inversa, che è:
Sommando, pertanto, AH e HB otterremo la base maggiore AB.
Ora, facilmente possiamo calcolare la base minore DC. Da AB dobbiamo sottrarre la misura di AK e HB (che misurano entrambe 9) :
A questo punto lascio concludere a te il calcolo di area e perimetro.
Se c'è qualcosa che non è chiaro, gradirei me lo facessi sapere.

Osserviamo attentamente la figura. Il testo ci dice che AC è perpendicolare al lato obliquo (per esempio CB). Cosa significa? Che il punto d'insersezione tra CB e la diagonale genera quella condizione per la quale il triangolo ABC è rettangolo, poiché l'angolo stesso in C è retto. Per quanto concerne una delle due misure che conosciamo, CH, essa non corrisponde ad altro che all'altezza relativa all'ipotenusa del triangolo ABC. E poiché noi conosciamo quest'ultima e il lato obliquo CB (uno dei due cateti del medesimo triangolo), possiamo calcolare la misura dell'ipotenusa, che in questo caso equivale alla misura della base maggiore AB. Su questo punto arriveremo tra poco. Concentriamoci ora sul triangolo CHB. Di esso conosciamo cateto (CH) e CB (ipotenusa). Possiamo, mediante l'applicazione del teorema di Pitagora, calcolare HB, l'altro cateto:
[math]\sqrt{CB^2 - CH^2} = \sqrt{15^2 - 12^2} = \sqrt{225 - 144} \to \sqrt{81} = 9 cm.[/math]
Ora, riprendendo il punto che ho lasciato in sospeso, riconsideriamo il triangolo ABC: abbiamo bisogno di applicare il secondo teorema di Euclide (che ti consiglio vivamente di ripassare), il quale afferma che "In un triangolo rettangolo, il quadrato costruito sull’altezza relativa all’ipotenusa è equivalente al rettangolo che ha per dimensioni le proiezioni dei cateti sull’ipotenusa."
[math]CH^2 = AH \cdot HB[/math]
Di questi dati, noi ne conosciamo due, pertanto dobbiamo svolgere la formula inversa, che è:
[math]AH = \frac{CH^2}{HB} = \frac{225}{9} = 25 cm [/math]
Sommando, pertanto, AH e HB otterremo la base maggiore AB.
[math]AB = AH + HB \to 25 + 9 = 36 cm[/math]
Ora, facilmente possiamo calcolare la base minore DC. Da AB dobbiamo sottrarre la misura di AK e HB (che misurano entrambe 9) :
[math]DC = AB - AK - HB \to 36 - 9 - 9 = 18 cm[/math]
A questo punto lascio concludere a te il calcolo di area e perimetro.
Se c'è qualcosa che non è chiaro, gradirei me lo facessi sapere.


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo