Implicazioni
Buon giorno a tutti.
Ho i seguenti enunciati:
a: gli asini volano
b: Milano è una citta svizzera
c: il gatto è un felino
L'enunciato a --> b (se gli asini volano allora Milano è una città svizzera) è vero.
L'enunciato c --> a (se il gatto è un felino allora gli asini volano) è falso
L'enunciato a --> c (se gli asini volano allora il gatto è un felino) è vero ma questo non lo capisco
Fausto
Ho i seguenti enunciati:
a: gli asini volano
b: Milano è una citta svizzera
c: il gatto è un felino
L'enunciato a --> b (se gli asini volano allora Milano è una città svizzera) è vero.
L'enunciato c --> a (se il gatto è un felino allora gli asini volano) è falso
L'enunciato a --> c (se gli asini volano allora il gatto è un felino) è vero ma questo non lo capisco
Fausto
Risposte
Quando l'ipotesi "gli asini volano" è falsa l'implicazione è vera in ogni caso, sia quando la tesi è vera "il gatto è un felino", sia quando è falsa "Milano è una città svizzera".
mi permetto di dare qualche dettaglio in più alla corretta risposta di @melia.
Nella seguente tabella di verità vediamo quando l'operatore logico "implicazione" è vero oppure falso in corrispondenza dei valori logici di A e B
La spiegazione della tabella si può verificare subito con un diagramma di Venn
(clic per ingrandire)
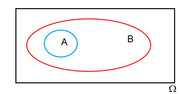
nel diagramma ho indicato una generica situazione in cui $A rarr B$, ovvero:
Come puoi agevolemente verificare, i costituenti dell'universo diagrammato sono soltanto 3:
Quindi l'unica combinazione Falsa (impossibile) è quando A e vero e B è falso
@fausto1947: per favore, le [formule][/formule]....
Non mi riferisco in particolare a questo messaggio ma agli altri postati e, soprattutto, agli eventuali futuri.
Già che ci siamo ti invito a leggere bene il punto 3.7 del [regolamento]3_7[/regolamento]
grazie
Nella seguente tabella di verità vediamo quando l'operatore logico "implicazione" è vero oppure falso in corrispondenza dei valori logici di A e B
| A | B | A "implica" B |
|---|---|---|
| Falso | Vero | Falso |
| Vero | Vero | Falso |
| Vero | Vero | Vero |
La spiegazione della tabella si può verificare subito con un diagramma di Venn
(clic per ingrandire)

nel diagramma ho indicato una generica situazione in cui $A rarr B$, ovvero:
la verità di $A$ è condizione sufficiente (ma non necessaria) per la verità di $B$ mentre la verità di $B$ è condizione necessaria (ma non sufficiente) per la verità di $A$.
Come puoi agevolemente verificare, i costituenti dell'universo diagrammato sono soltanto 3:
| A | B | Costituente |
|---|---|---|
| Falso | Fuori da B | Falso |
| Fuori da A ma dentro B | Vero | Vero |
Quindi l'unica combinazione Falsa (impossibile) è quando A e vero e B è falso
@fausto1947: per favore, le [formule][/formule]....

Non mi riferisco in particolare a questo messaggio ma agli altri postati e, soprattutto, agli eventuali futuri.
Già che ci siamo ti invito a leggere bene il punto 3.7 del [regolamento]3_7[/regolamento]
grazie
Grazie delle risposte,
capisco che la tavola della verità ed i diagrammi di Venn dicano che sia vero, ma allora perchè sia la lingua italiana che la mia mente mi portano a considerarlo falso?
Fausto
capisco che la tavola della verità ed i diagrammi di Venn dicano che sia vero, ma allora perchè sia la lingua italiana che la mia mente mi portano a considerarlo falso?
Fausto
non so la tua mente, ma la lingua italiana, come credo anche le altre lingue, mi pare in accordo con le implicazioni mostrate. Spesso l'umorismo si basa sulla logica, cosa ne dici di questa:
"Se Parigi avesse il mare, sarebbe una piccola Bari"
"Se Parigi avesse il mare, sarebbe una piccola Bari"


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo