Successioni e basi
La successione crescente 1,3,4,9,10,.... è composta da interi positivi che sono potenze di 3 o somma di distinte potenze di 3.
a) Sapreste trovare il 50° termine e il 100° termine della successione?
b) Sapreste trovare un modo per ricavare l'n-esimo termine della successione?
NB:il 1° termine è 1, il 2° è 3,....
a) Sapreste trovare il 50° termine e il 100° termine della successione?
b) Sapreste trovare un modo per ricavare l'n-esimo termine della successione?
NB:il 1° termine è 1, il 2° è 3,....
Risposte
Se consideriamo n valori la successione sarà composta da:
n + (n-1) + (n-2) .... + 1 valori
Creando un piccolo programma mi sono usciti questi valori:
50° 1125
100° 3376
500° 37648
1000° 106597
n + (n-1) + (n-2) .... + 1 valori
Creando un piccolo programma mi sono usciti questi valori:
50° 1125
100° 3376
500° 37648
1000° 106597
Due piccole obiezioni:
1)La soluzione non è esatta
2)Quando ho scritto "metodo per ricavare l'n-esimo termine" intendevo una formula chiusa o qualcosa che associ ad n il suo $a_n$ in modo univoco...
1)La soluzione non è esatta
2)Quando ho scritto "metodo per ricavare l'n-esimo termine" intendevo una formula chiusa o qualcosa che associ ad n il suo $a_n$ in modo univoco...
50°=325
100°=976
Se è giusto, posto la soluzione, appena riesco a scriverla in maniera formale (per ora è molto "naif")
100°=976
Se è giusto, posto la soluzione, appena riesco a scriverla in maniera formale (per ora è molto "naif")
Non è giusto ma l'errore è abbastanza piccolo, quindi prova a postare la soluzione che hai... può essere un semplice errore di calcolo...
"Jack233":
Due piccole obiezioni:
1)La soluzione non è esatta
2)Quando ho scritto "metodo per ricavare l'n-esimo termine" intendevo una formula chiusa o qualcosa che associ ad n il suo $a_n$ in modo univoco...
Le obiezioni sono sempre le benvenute, permettono di confrontarci, e spesso sono utili a ricercare la soluzione.
Al punto 1) dici che le soluzioni non sono esatte. Cio' significa che conosci quelle giuste ? Quali sono ?
Per quanto riguarda il punto 2) non sempre è possibile trovare una formula (.. cio' non significa che nel tuo caso non ci sia ..), ma solo che ho preferito dare in pasto 4 istruzioni al mio pc, per una soluzione piu immediata.
$x_{50}=327, x_{100}=981$?
"Umby":
[quote="Jack233"]Due piccole obiezioni:
1)La soluzione non è esatta
2)Quando ho scritto "metodo per ricavare l'n-esimo termine" intendevo una formula chiusa o qualcosa che associ ad n il suo $a_n$ in modo univoco...
Le obiezioni sono sempre le benvenute, permettono di confrontarci, e spesso sono utili a ricercare la soluzione.
Al punto 1) dici che le soluzioni non sono esatte. Cio' significa che conosci quelle giuste ? Quali sono ?
Per quanto riguarda il punto 2) non sempre è possibile trovare una formula (.. cio' non significa che nel tuo caso non ci sia ..), ma solo che ho preferito dare in pasto 4 istruzioni al mio pc, per una soluzione piu immediata.[/quote]
Le soluzioni le so, infatti il topic non è del tipo "aiuto, non riesco a risolvere", è un problema che ho risolto e che volevo postare... Per la formula, è vero che non sempre è possibile ricavare una formula (per esempio in questo problema la formula è brutta da scrivere...) tuttavia sono graditi ragionamenti e anche istruzioni da pc, magari con qualche nota (che so, tipo "ho notato che se n è di questo tipo allora...")...
@Wizard: Risposta esatta
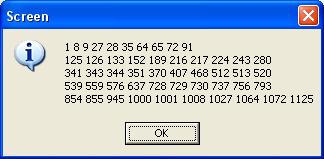
Il mio 1125 nasce da:
$n^3$ per n=1, 2, 3, 4 ....... piu' le sommatorie (senza ripetizioni) dei singoli termini
Forse nel quesito si intendeva:
$3^n$ e non $n^3$
$n^3$ per n=1, 2, 3, 4 ....... piu' le sommatorie (senza ripetizioni) dei singoli termini

Forse nel quesito si intendeva:
$3^n$ e non $n^3$
Si vogliono trovare gli elementi di posto $50$ e $100$ della successione i cui primi termini sono $1,3,4,9,10$ e il cui termine generale o è potenza di $3$ o è somma di potenze di $3$ tutte contate una sola volta.
Siano $nk$ sono esattamente $2^{k}$ (anche qui basta usare un poco di calcolo combinatorio se si vuole ottenere un convincimento formale): i.e. c'è un unico termine $3^{n}+3^{0}$ senza potenze di $3$ con esponente maggiore di $0$ (e minori di $n$), ci sono due termini $3^{n}+3^{1}$ senza potenze di $3$ maggiori $1$ (e minori di $n$; vale a dire $3^{n}+3^{1}$ medesimo e $3^{n}+3^{1}+3^{0}$) e così continuando.
Detto ciò, si capisce che il termine $x_{50}$ è compreso tra $3^{5}$ e $3^{6}$, perché $2^{5}=32<50<64=2^{6}$; il termine di posizione $50$ è il $18$-esimo termine successivo al termine di posizione $32$ (i.e. $3^{5}=243$) e tenendo conto di quanto prima detto risulta essere il terzo termine tra i termini ottenuti con la potenza $3^{4}$ sena potenze magiori di questa e minori di $3^{5}$: i.e. $x_{50}=3^{5}+3^{4}+3^{0}=327$.
Analogamente per $x_{100}$.
Quanto alla formula chiusa non sono in grado di trovarla.
Siano $n
Detto ciò, si capisce che il termine $x_{50}$ è compreso tra $3^{5}$ e $3^{6}$, perché $2^{5}=32<50<64=2^{6}$; il termine di posizione $50$ è il $18$-esimo termine successivo al termine di posizione $32$ (i.e. $3^{5}=243$) e tenendo conto di quanto prima detto risulta essere il terzo termine tra i termini ottenuti con la potenza $3^{4}$ sena potenze magiori di questa e minori di $3^{5}$: i.e. $x_{50}=3^{5}+3^{4}+3^{0}=327$.
Analogamente per $x_{100}$.
Quanto alla formula chiusa non sono in grado di trovarla.
Ho elaborato fino a $3^9$.
La serie si compone di 1023 elementi, ovvero $(2^(n+1))-1$
327 e 981 anche per me.
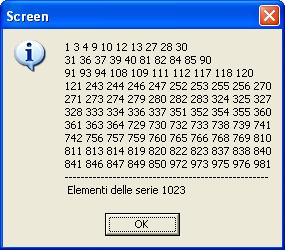
La serie si compone di 1023 elementi, ovvero $(2^(n+1))-1$
327 e 981 anche per me.

Se scriviamo la serie cosi', ci rendiamo conto che la serie puo' essere scomposta in forma binaria, ed ad ogni carattere binario gli diamo un peso di potenza di 3.
1
3 ---> il secondo elemento (1-0 in binario è pari a $1*3^1+0*3^0$)
4 9
10 12 13 27 ---> il settimo elemento (1-1-1 in binario è pari a $1*3^2+1*3^1+1*3^0$ = 9+3+1 = 13)
28 30 31 36 37 39 40 81
Pertanto:
50 in binario: 1-1-0-0-1-0 e quindi:
$1*3^5+1*3^4+0*3^3+0*3^2+1*3^1+0*3^0$ = 243+81+3 = 327
1
3 ---> il secondo elemento (1-0 in binario è pari a $1*3^1+0*3^0$)
4 9
10 12 13 27 ---> il settimo elemento (1-1-1 in binario è pari a $1*3^2+1*3^1+1*3^0$ = 9+3+1 = 13)
28 30 31 36 37 39 40 81
Pertanto:
50 in binario: 1-1-0-0-1-0 e quindi:
$1*3^5+1*3^4+0*3^3+0*3^2+1*3^1+0*3^0$ = 243+81+3 = 327
@Umby
Non mi dire niente ma non ti ho capito
Non mi dire niente ma non ti ho capito
Tralasciando le osservazioni fatte per raggiungere il risultato, la formula è semplicissima.
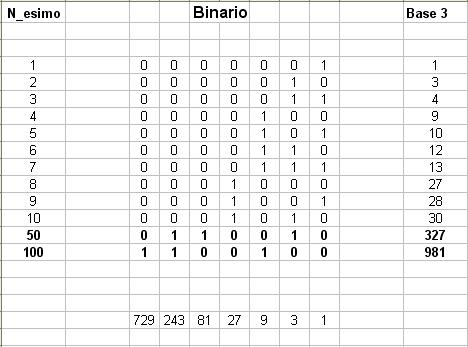
- Converti in binario l'ennesimo elemento
- Riconverti il binario in base 3
La tabella mostra i primi 10 elementi della serie,
il 50esimo, ed il 100esimo (oggetti della discussione)
- Converti in binario l'ennesimo elemento
- Riconverti il binario in base 3
La tabella mostra i primi 10 elementi della serie,
il 50esimo, ed il 100esimo (oggetti della discussione)

Avevo inteso che il metodo che indicavi fosse questo. Non mi è però chiaro il motivo teorico che fa funzionare questa regola.
In pratica tu cambi da base 10 a base 2 il numero che indica la posizione nella successione di un certo elemento, poi sostituisci alle potenze di 2 le potenze do 3 e ottieni l'elemento in base 10 che si trova in quella posizione.
Non riesco a capire il motivo teorico che fa funzionare questa brillante intuizione.
In pratica tu cambi da base 10 a base 2 il numero che indica la posizione nella successione di un certo elemento, poi sostituisci alle potenze di 2 le potenze do 3 e ottieni l'elemento in base 10 che si trova in quella posizione.
Non riesco a capire il motivo teorico che fa funzionare questa brillante intuizione.
La binaricità nasce dal quesito stesso, ovvero dal fatto che i termini delle somme possono essere presi solo una volta (quindi c'è o non c'è --> 0 o 1 ). D'altronde fin dall'inizio era apparso chiaro che il numero di elementi della serie era potenza di 2. Se riprovi a fare lo stesso esercizio utilizzando la base 10 anzichè la 3 (1 10 11 100 101 ......) il concetto sarà più evidente.
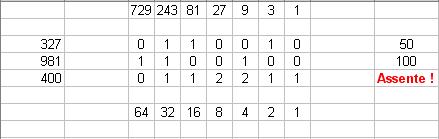
Simpatica la formula inversa:
E' possibile non solo stabilire in che posizione si trova un certo numero, ma anche se il numero fa parte o meno della serie. La presenza di un "2" (in base 3) determina l'assenza del numero stesso (vedi 400).
Simpatica la formula inversa:
E' possibile non solo stabilire in che posizione si trova un certo numero, ma anche se il numero fa parte o meno della serie. La presenza di un "2" (in base 3) determina l'assenza del numero stesso (vedi 400).

Ok. Grazie mille!


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo