Intersezione di cerchi

[ficus2002]

Sia dato un triangolo equilatero inscritto in una circonferenza di raggio $R$. Siano $D_0, D_1, D_2$ tre cerchi (senza bordo) di raggio $R$ centrati nei vertici del triangolo. Dimostrare che $D_0 \cap D_1 \cap D_2 = \emptyset$.

[elgiovo]

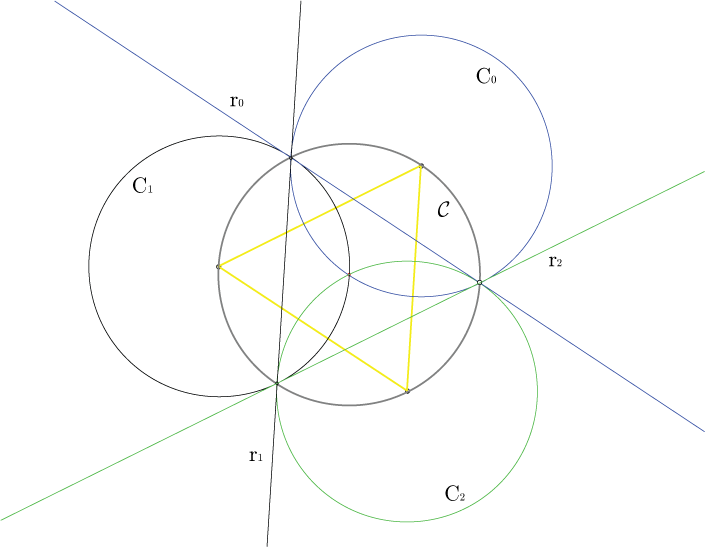
Le tre circonferenze $C_0$, $C_1$ e $C_2$ hanno lo stesso raggio $R$ della circonferenza $ccC$
circoscritta al triangolo e sono centrate su di essa, dunque passano tutte e tre per il suo centro.
Applicando un'inversione proprio in $ccC$ si ottengono le tre rette $r_0$, $r_1$ ed $r_2$.
Infatti invertendo in una circonferenza un'altra circonferenza passante per il centro della prima,
si ottiene una retta passante per i punti di intersezione delle due circonferenze.
Analogamente, i cerchi $D_0$, $D_1$ e $D_2$ sono mappati dall'inversione in semipiani
delimitati proprio dalle rette $r_0$, $r_1$ ed $r_2$ (in particolare, i punti di $D_0$ che stanno
a destra di $r_0$ sono mappati proprio nella parte di cerchio a destra di $r_0$, mentre
i punti di $D_0$ a sinistra di $r_0$ sono mappati nella parte rimanente di semipiano).
Detti $ccS_0$, $ccS_1$ e $ccS_2$ i semipiani, è facile notare che $ccS_0 cap ccS_1 cap ccS_2 = emptyset$, da cui la tesi.

[zorn1]

Bel quesito! Allora, bisogna dimostrare che le tre circonferenze (considero il bordo) si toccano nel circocentro. Per questo basta osservare che, essendo il triangolo equilatero, la distanza di un vertice dal circocentro è pari ad $R$, e si conclude facilmente.

[Sk_Anonymous]

"elgiovo":
Le tre circonferenze $C_0$, $C_1$ e $C_2$ hanno lo stesso raggio $R$ della circonferenza $ccC$
circoscritta al triangolo e sono centrate su di essa, dunque passano tutte e tre per il suo centro.

Pare che la cosa sia stata gia' considerata da Elgiovo

[ficus2002]

Bella la soluzione di Elgiovo;
@ zorn
Bisognerebbe dimostrare che l'intersezione dei cerchi chiusi consiste di solo quel punto;

Cmq, questo problema mi è stato suggerito da questo fatto:
Siano $D_i\subseteq CC,\quad i=0,1,2$ i tre dischi aperti unitari centrati nelle radici cubiche dell'unità. Siano $f_i\in H(D_i),\quad i=0,1,2$ tali che $f_i^2(z)=z,\quad \forall z\in D_i$ e tali che
$f_0|D_0\cap D_1=f_1|D_0\cap D_1$ e
$f_1|D_1\cap D_2=f_2|D_1\cap D_2$.
Allora $f_2|D_2\cap D_0=-f_0|D_2\cap D_0$. In particolare, questo dimostra che $D_0\cap D_1\cap D_2=\emptyset$.