6 monete

[Paolo k]

Ho 6 monete, una è falsa, quella falsa ha un peso diverso da quelle vere ma non si sa se pesi di più o di meno. Come posso determinare quale sia la moneta falsa e se pesi di più o di meno con tre pesate su una bilancia di precisione che indichi esattamente il peso delle monete?

[poliaficostefano]

Ho ragionato un bel po', ma occorrono per forza 4 pesate...

[giammaria2]

Il testo fa pensare ad una bilancia ad un piatto, ed allora non so se è possibile e come; rispondo riferendomi ad una bilancia a due piatti.

Metto due monete su un piatto ed altre due sull'altro.
- Se i piatti hanno lo stesso peso, la moneta falsa è una delle altre due e ne confronto una con una delle buone. Se è diversa, so che è falsa e se è più leggera o più pesante; altrimenti ripeto la cosa con l'altra moneta.
- Se i due piatti hanno peso diverso, sostituisco le monete del piatto leggero con le due finora non pesate. Se ora i piatti sono in equilibrio, la moneta falsa era una di quelle del piatto leggero ed è più leggera delle buone; la individuo confrontando una di esse con una buona. Altrimenti, la moneta falsa era una del piatto più pesante ed è più pesante; la individuo come prima.

[chrave]

Devi pesare prima quattro monete (magari 1 2 3 4) poi tre monete magari (1 2 5). Confrontando le medie capisci se ne hai pesata una con peso diverso dalle altre.

A questo punto devi fare una pesata con la 6 e un'altra che varia a seconda dei risultati ottenuti in precedenza.

Avevo fatto uno schema, se lo ritrovo lo spedisco.

[bimbinoGio]

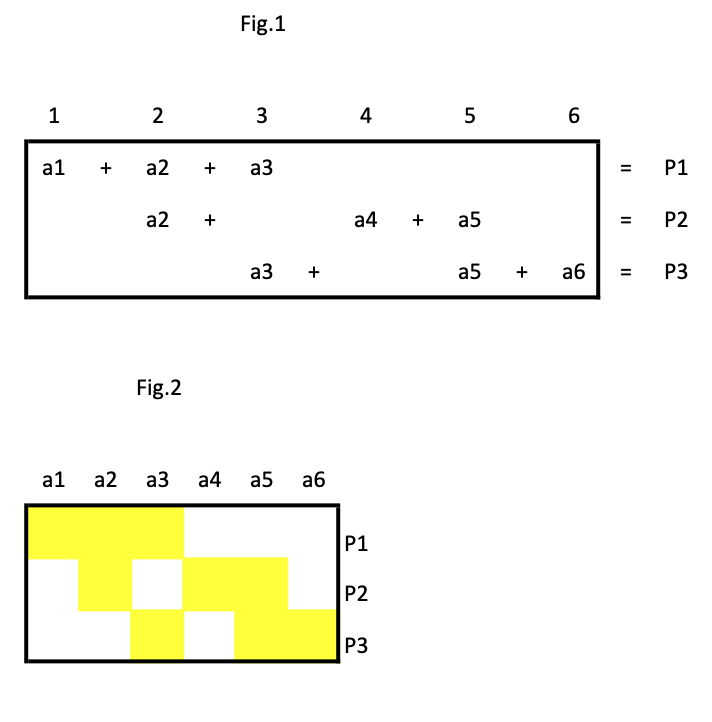
Abbiamo le monete aj (per j=1,2,…,6) con le quali facciamo le pesate Pi (per i=1,2,3). Costruiamo la tabella TP delle pesate P1=a1+a2+a3, P2=a2+a4+a5 e P3=a3+a5+a6 come illustrato nella Fig.1, oppure più sinteticamente, eliminando i simboli + e = come illustrato in Fig.2, dove una casella gialla indica l’esistenza di una moneta.
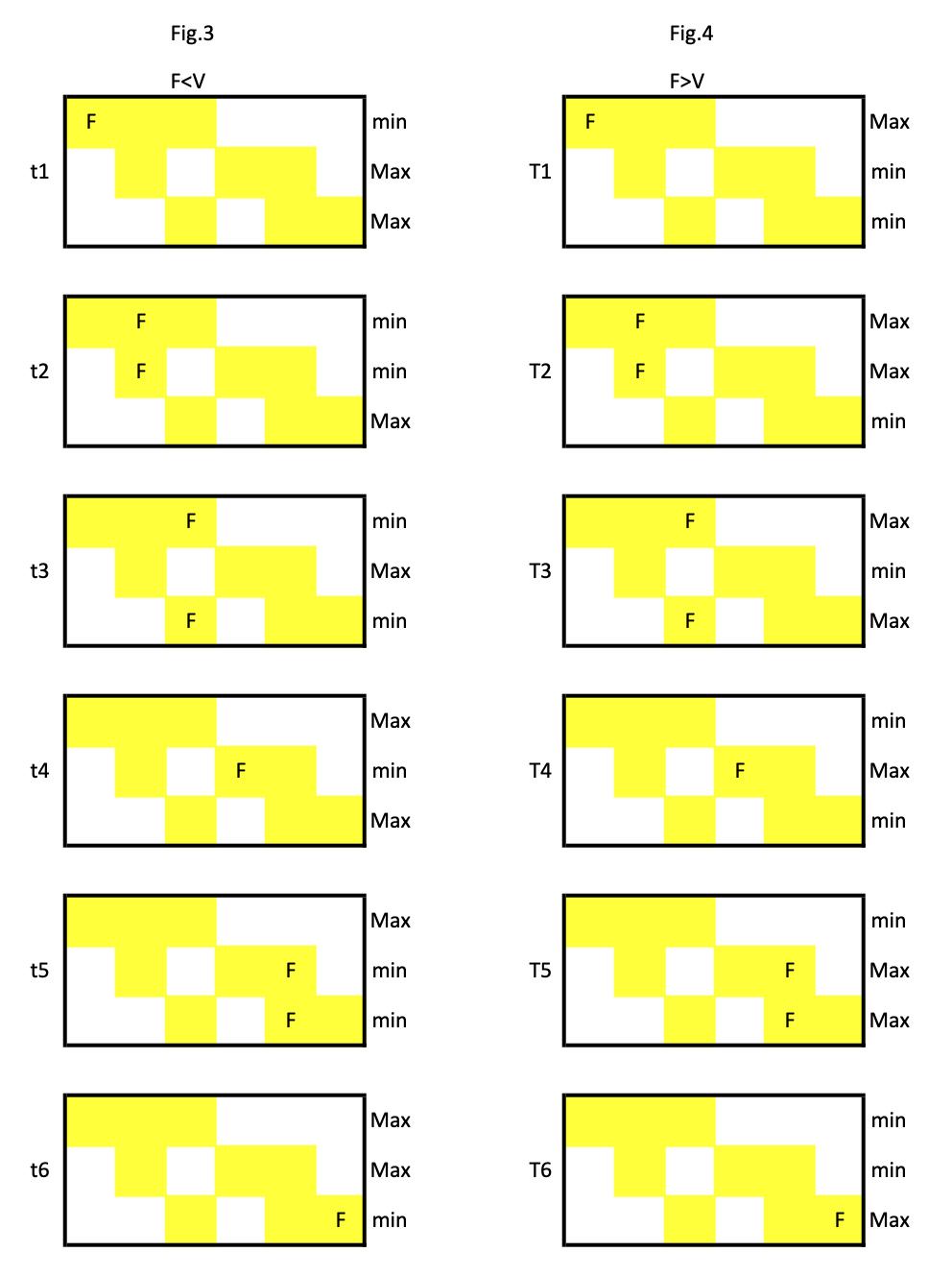
Se le monete avessero tutte lo stesso peso avremmo P1=P2=P3 ma una moneta (che indichiamo con F mentre le altre sono V) ha un peso diverso. Non sappiamo in quale colonna di TP sia F per cui facciamo le 12 tabelle con tutti i casi possibili. In Fig.3 F < V e in Fig.4 F > V.
Nelle tre pesate le righe con F daranno un risultato diverso da quelle con monete tutte vere. Indichiamo con min un risultato Pi se esso è il minore dei tre, con Max se esso è il maggiore dei tre. Vediamo come in un caso pratico si trova la soluzione.
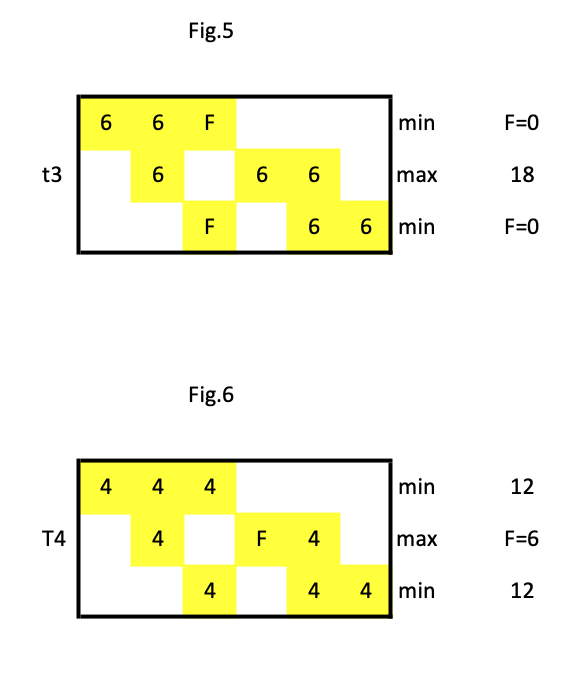
Supponiamo di aver avuto:
P1=12=min
P2=18=Max
P3=12=min
a cui corrispondono le tabelle t3 e T4 (vedi Fig.5 e Fig.6), ma se mettiamo i valori delle monete in modo da ottenere i pesi dell’ipotesi vediamo che solo T4 ha senso, quindi la moneta falsa è a4 e pesa di più di quella vera. Purtroppo se inserisco l'immagine viene una cosa troppo piccola per cui uso un allegato.
Un po' tardi vedo un errore: in Fig.6 ho scritto F=6 invece di F=10...

SLx7siNVroqTIuy2_1762705642.jpg

Provo ancora con l'immagine, forse dipendeva dal fatto che era troppo larga.

Direi che ci siamo, sono ancora un novellino su questo sito.

[bimbinoGio]

Ritiro tutto, mi hanno fatto notare che non funziona sempre :(

[apatriarca]

Secondo me non è possibile. Facendo tre pesate con lo stesso numero di monete otterremo uno o due valori. Siccome non sappiamo se la moneta falsa pesa più o meno delle altre, non abbiamo modo a priori di sapere se sia contenuta nelle pesate con valore maggiore o minore. Possiamo quindi solo distinguere i casi in base a quali valori sono uguali:

1. P1 = P2 = P3
2. P1 = P2 != P3
3. P1 = P3 != P2
4. P1 != P2 = P3

È quindi possibile ottenere solo 4 risposte diverse, non abbastanza per risolvere il problema. Sapendo se la moneta falsa pesa più o meno delle altre, avremmo invece 7 casi possibili.

[apatriarca]

Ripensandoci, credo che @chrave abbia ragione. È necessario usare pesate con un numero diverso di monete. In questo modo le differenze tra le medie ci forniscono indizi aggiuntivi. Le prime due pesate sono P1 = P(1, 2, 3, 4) e P2 = P(1, 2, 5). Se 3P1 = 4P2, allora la moneta 6 è quella falsa; la pesiamo e la confrontiamo con V = P1/4 per sapere se è più leggera o più pesante. Di seguito suppongo che il peso di una moneta vera sia V e quello di una moneta falsa sia F = V + x. Inoltre, facciamo la terza pesata P3 = P(1, 3). I risultati sono mostrati in tabella:

FALSA |   P1   |   P2   |   P3   | 3P1 - 4P2 | 2P1 - 4P3 | 2P2 - 3P3 |
------+--------+--------+--------+-----------+-----------+-----------+
1     | 4V + X | 3V + X | 2V + X |    - X    |    -2X    |    -X     |
2     | 4V + X | 3V + X |   2V   |    - X    |     2X    |    2X     |
3     | 4V + X |   3V   | 2V + X |     3X    |    -2X    |   -3X     |
4     | 4V + X |   3V   |   2V   |     3X    |     2X    |     0     |
5     |   4V   | 3V + X |   2V   |    -4X    |      0    |    2X     |
6     |   4V   |   3V   | V + X* |      0    |    -4X    |   -3X     |
------+--------+--------+--------+-----------+-----------+-----------+  

Come vedi i diversi coefficienti ci permettono di distinguere i 6 casi.