[LaTeX] Diagrammi
Come si fanno diagrammi tipo questi?
Risposte
io faccio tutto diversamente, e penso che Stan possa aggiungere anche questa estensione proprio per MathJax ma il profi é lui, io ho solo smanettato un pochino, e mi aspetto una romanzina per le eventuali imprecisioni che dico... 
Scrivo solo la seguente per come faccio io a visualizzare alcuni diagrammi..
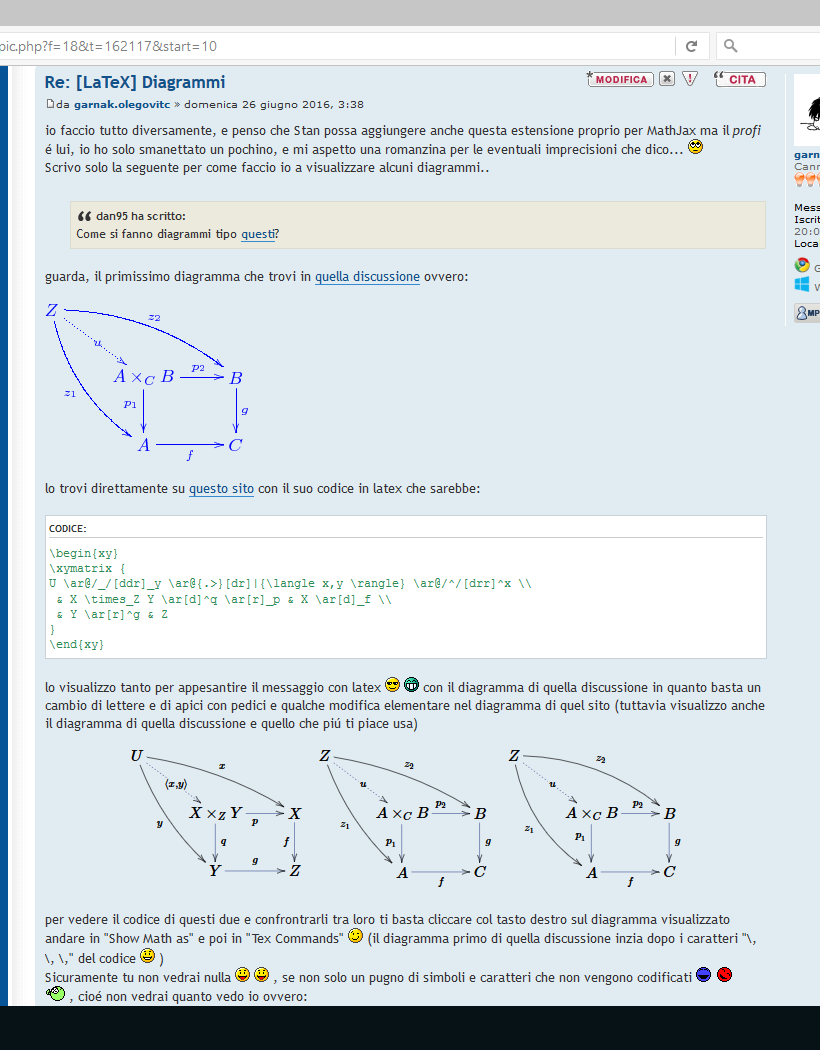
guarda, il primissimo diagramma che trovi in quella discussione ovvero:
[tex]\xymatrix{
Z \ar@/_10pt/[ddr]_{z_1} \ar@/^10pt/[drr]^{z_2} \ar@{.>}[dr]|{u} & & \\
& A\times_C B \ar[d]_(0.4){p_1} \ar[r]^(0.6){p_2} & B \ar[d]^{g}\\
& A \ar[r]_{f} & C
}[/tex]
lo trovi direttamente su questo sito con il suo codice in latex che sarebbe:
lo visualizzo tanto per appesantire il messaggio con latex
con il diagramma di quella discussione in quanto basta un cambio di lettere e di apici con pedici e qualche modifica elementare nel diagramma di quel sito (tuttavia visualizzo anche il diagramma di quella discussione e quello che piú ti piace usa)
\[
\begin{xy}
\xymatrix {
U \ar@/_/[ddr]_y \ar@{.>}[dr]|{\langle x,y \rangle} \ar@/^/[drr]^x \\
& X \times_Z Y \ar[d]^q \ar[r]_p & X \ar[d]_f \\
& Y \ar[r]^g & Z
}
\end{xy} \, \, \, \begin{xy}
\xymatrix {
Z \ar@/_/[ddr]_{z_1} \ar@{.>}[dr]|{u} \ar@/^/[drr]^{z_2} \\
& A \times_C B \ar[d]_{p_1} \ar[r]^{p_2} & B \ar[d]^g \\
& A \ar[r]_f & C
}
\end{xy} \, \, \, \xymatrix{
Z \ar@/_10pt/[ddr]_{z_1} \ar@/^10pt/[drr]^{z_2} \ar@{.>}[dr]|{u} & & \\
& A\times_C B \ar[d]_(0.4){p_1} \ar[r]^(0.6){p_2} & B \ar[d]^{g}\\
& A \ar[r]_{f} & C
}
\]per vedere il codice di questi due e confrontrarli tra loro ti basta cliccare col tasto destro sul diagramma visualizzato andare in "Show Math as" e poi in "Tex Commands"
(il diagramma primo di quella discussione inzia dopo i caratteri "\, \, \," del codice 
)
Sicuramente tu non vedrai nulla
, se non solo un pugno di simboli e caratteri che non vengono codificati 
, cioé non vedrai quanto vedo io ovvero:
come mai? Semplice, non é vero, come ho detto prima, che "basta un cambio di lettere e di apici con pedici e qualche modifica elementare", ti occorrono (nel caso in cui usi Google Chrome) questa estensione e il primo script, visualizzando il codice, usato in questa pagina[nota](preso da https://github.com/sonoisa/XyJax/blob/master/README.md, XyJax é una estensione per Mathjax ancora in sviluppo, se ho letto bene, ma che si puó giá usare
[/nota]
Segui, se sei interessato, le sguenti procedure:
-1- installa l´estensione
-2- finita l´installazione, clicca col tasto sx sulla estensione e poi lá dove ho cerchiato in rosso nell´immagine seguente (scusa ma io ormai uso e parlo tedesco ovunque, in italiano dovresti tramite l´immagine individuare la voce facilmente):
-3- ti verrá aperta una finestra come la seguente:
cancella tutto quello che vi é scritto nel riquadro bianco ed incolla il seguente codice (nel quale viene inglobato lo script citato prima)
adesso hai finito e se ricarichi la pagina di questa discussione dovresti visualizzare i digrammi (preciso che puó capitare che a primo uso non visualizza un tubo allora ricarica la pagina che dovrebbe andare , che dire? Sempre meglio di niente o almeno per le frecce curve e alcune in diagonale poiché proprio per queste si usa questa estensione (http://meta.math.stackexchange.com/questions/14986/is-it-possible-to-draw-a-diagonal-arrow-in-a-commutative-diagram/14987#14987))
Inoltre nella pagina di prima, ovvero questa, trovi tanti esempi dai quali puoi partire, alcuni sono fantastici come quello del metodo di Newton,... ad esempio:
http://sonoisa.github.io/xyjax/xyjax.ht ... rixFeature (il quinto diagramma é fantastico poterlo visualizzare online con tanto di codice LaTex e a colori anche)
http://sonoisa.github.io/xyjax/xyjax.ht ... on'sMethod
http://sonoisa.github.io/xyjax/xyjax.ht ... seFunction
per il tuo digramma postato dopo, se hai seguito i passi di sopra, si ha con uno stile migliore, poiché anche l´occhio vuole la sua parte, la seguente:
$$ \xymatrix{ &\pi_1(A) \ar[rd]^{i_{\ast}} \\\pi_1(A\cap B) \ar[ru]^{\alpha_{\ast}} \ar[rd]_{\beta_{ \ast}} &&\pi_1(A\cup B) \\&\pi_1(B) \ar[ru]_{j_{\ast}} } $$
Esiste la stessa estensione anche per Firefox, quella uso io é questa, sinceramente lavora meglio su Mozilla che su Chrome (ovviamente parlo per me e per le versioni di Chrome e Mozilla che ho ed uso), lo script é lo stesso e per aggiugerlo si seguono gli stessi identici passi di prima
ps.=volendo visualizzare questo diagramma:
coi i delimitatori "tex" si ha:
[tex]\xymatrix{ & T(TM) & T^\ast(T^\ast M) \\ & T^\ast M \ar_{X_H} \ar[ur]_{\theta_H} \\ \mathbb R \ar@/^2pc/[uur]^{X_H\circ(\alpha\circ\phi)} \ar@/^1pc/[ur]^{\alpha\circ\gamma} \ar[r]^{\gamma} \ar@/_1pc/[dr]_{x\circ\gamma} \ar@/_2pc/[ddr]_{x_\iota\circ(x\circ\gamma)} & M \ar[d]_x \\ & TM \ar[d]_{X_\iota} \ar[dr]^{\theta_n} \\ & T(TM) & T^\ast(TM) }[/tex]
usando lo script l´aspetto migliora:
\(\xymatrix{ & T(TM) & T^\ast(T^\ast M) \\ & T^\ast M \ar_{X_H} \ar[ur]_{\theta_H} \\ \mathbb R \ar@/^2pc/[uur]^{X_H\circ(\alpha\circ\phi)} \ar@/^1pc/[ur]^{\alpha\circ\gamma} \ar[r]^{\gamma} \ar@/_1pc/[dr]_{x\circ\gamma} \ar@/_2pc/[ddr]_{x_\iota\circ(x\circ\gamma)} & M \ar[d]_x \\ & TM \ar[d]_{X_\iota} \ar[dr]^{\theta_n} \\ & T(TM) & T^\ast(TM) }\)
per chi non usa lo script puó vedere qui
oppure:
[tex]\xymatrix{ & & & C_1 \ar[rr]^{\gamma_1} \ar[dd]_(.6){f^\prime} & & C_2 \ar[dd]_(.6){g^\prime} \ar[rr]^{\gamma_2} & & C_3 \ar[rr] \ar[dd]_(.6){h^\prime} & & 0 \\ & & A_1 \ar[dd]^(.4)f \ar[ur]^{k_1} \ar[rr]^(.6){\alpha_1} & & A_2 \ar[ur]^{k_2} \ar[dd]^(.4)g \ar[rr]^(.6){\alpha_2} & & A_3 \ar[ur]^{k_3} \ar[dd]^(.4)h \ar[rr] & & 0 \\ & 0 \ar[rr] & & D_1 \ar[rr]^(.4){\delta_1} & & D_2 \ar[rr]^(.4){\delta_2} & & D_3 \\ 0 \ar[rr] & & B_1 \ar[rr]^{\beta_1} \ar[ur]^{j_1} & & B_2 \ar[ur]^{j_2} \ar[rr]^{\beta_2} & & B_3 \ar[ur]^{j_3} }[/tex]
\[\xymatrix{ & & & C_1 \ar[rr]^{\gamma_1} \ar[dd]_(.6){f^\prime} & & C_2 \ar[dd]_(.6){g^\prime} \ar[rr]^{\gamma_2} & & C_3 \ar[rr] \ar[dd]_(.6){h^\prime} & & 0 \\ & & A_1 \ar[dd]^(.4)f \ar[ur]^{k_1} \ar[rr]^(.6){\alpha_1} & & A_2 \ar[ur]^{k_2} \ar[dd]^(.4)g \ar[rr]^(.6){\alpha_2} & & A_3 \ar[ur]^{k_3} \ar[dd]^(.4)h \ar[rr] & & 0 \\ & 0 \ar[rr] & & D_1 \ar[rr]^(.4){\delta_1} & & D_2 \ar[rr]^(.4){\delta_2} & & D_3 \\ 0 \ar[rr] & & B_1 \ar[rr]^{\beta_1} \ar[ur]^{j_1} & & B_2 \ar[ur]^{j_2} \ar[rr]^{\beta_2} & & B_3 \ar[ur]^{j_3} }\]
clic qui per chi non usa lo script
UPDATE:
ed anche:
questo non riesco proprio a visualizzarlo senza estensione, ergo uso lo script direttamente:
\[
\xymatrix@C=2cm{
& & H(Z) \ar@/^2.0pc/[rr]^{F(f^{op} \circ g^{op})} \ar[r]^{H^{*}(g^{op})}
& H(Y) \ar@{=}[dl] \ar[r]^{H^{*}(f^{op})}
& H(X) \ar@{=}[dl] \ar@/^2.0pc/@{=>}[ddll] \\
& H(Z) \ar@{=}[ur]
& H(Y) \ar_{G(g^{op})}
& H(X) \ar@{=}[dl] \ar_{G(f^{op})} \\
H(Z) \ar[r]_{H^{*}(g^{op})} \ar@{=}[ur]
& H(Y) \ar@{=}[ur] \ar[r]_{H^{*}(f^{op})} \ar_{G(g^{op})}
& H(X) \ar_{G(f^{op})}
\ar@/^2.0pc/[uu]^{G(f^{op} \circ g^{op})}
}
\]
questi sono semplicissimi:
anche qui uso l´estensione:
\[\xymatrix{
A \ruppertwocell^f{\alpha}
\rlowertwocell_h{\beta}
\ar[r]|{g}
&B\\
} \]\[
\xymatrix{
& A \ar[d]^{i} \ar@{-->}[dl]_-{\exists \tilde{\varphi}} \\
B \ar[r]^{\varphi} &C
}
\]
qualcosa di anomalo come:
con lo script si ha:
\[\xymatrix{A \ar@(dr,dl)[r]\ar@(dr,dl)[rr]
&B\ar@(d,r)[dl] &C \\
E \ar@(ul,ur)} \]
per chi non usa lo script puó vedere qui
ps= lo script va in conflitto alle volte con la codifica Ascimathml usata da alcuni utenti, ergo visualizzo male le loro formule...
Scrivo solo la seguente per come faccio io a visualizzare alcuni diagrammi..
"dan95":
Come si fanno diagrammi tipo questi?
guarda, il primissimo diagramma che trovi in quella discussione ovvero:
[tex]\xymatrix{
Z \ar@/_10pt/[ddr]_{z_1} \ar@/^10pt/[drr]^{z_2} \ar@{.>}[dr]|{u} & & \\
& A\times_C B \ar[d]_(0.4){p_1} \ar[r]^(0.6){p_2} & B \ar[d]^{g}\\
& A \ar[r]_{f} & C
}[/tex]
lo trovi direttamente su questo sito con il suo codice in latex che sarebbe:
\begin{xy}
\xymatrix {
U \ar@/_/[ddr]_y \ar@{.>}[dr]|{\langle x,y \rangle} \ar@/^/[drr]^x \\
& X \times_Z Y \ar[d]^q \ar[r]_p & X \ar[d]_f \\
& Y \ar[r]^g & Z
}
\end{xy}
lo visualizzo tanto per appesantire il messaggio con latex
con il diagramma di quella discussione in quanto basta un cambio di lettere e di apici con pedici e qualche modifica elementare nel diagramma di quel sito (tuttavia visualizzo anche il diagramma di quella discussione e quello che piú ti piace usa)\[
\begin{xy}
\xymatrix {
U \ar@/_/[ddr]_y \ar@{.>}[dr]|{\langle x,y \rangle} \ar@/^/[drr]^x \\
& X \times_Z Y \ar[d]^q \ar[r]_p & X \ar[d]_f \\
& Y \ar[r]^g & Z
}
\end{xy} \, \, \, \begin{xy}
\xymatrix {
Z \ar@/_/[ddr]_{z_1} \ar@{.>}[dr]|{u} \ar@/^/[drr]^{z_2} \\
& A \times_C B \ar[d]_{p_1} \ar[r]^{p_2} & B \ar[d]^g \\
& A \ar[r]_f & C
}
\end{xy} \, \, \, \xymatrix{
Z \ar@/_10pt/[ddr]_{z_1} \ar@/^10pt/[drr]^{z_2} \ar@{.>}[dr]|{u} & & \\
& A\times_C B \ar[d]_(0.4){p_1} \ar[r]^(0.6){p_2} & B \ar[d]^{g}\\
& A \ar[r]_{f} & C
}
\]per vedere il codice di questi due e confrontrarli tra loro ti basta cliccare col tasto destro sul diagramma visualizzato andare in "Show Math as" e poi in "Tex Commands"
(il diagramma primo di quella discussione inzia dopo i caratteri "\, \, \," del codice )Sicuramente tu non vedrai nulla
, se non solo un pugno di simboli e caratteri che non vengono codificati , cioé non vedrai quanto vedo io ovvero: come mai? Semplice, non é vero, come ho detto prima, che "basta un cambio di lettere e di apici con pedici e qualche modifica elementare", ti occorrono (nel caso in cui usi Google Chrome) questa estensione e il primo script, visualizzando il codice, usato in questa pagina[nota](preso da https://github.com/sonoisa/XyJax/blob/master/README.md, XyJax é una estensione per Mathjax ancora in sviluppo, se ho letto bene, ma che si puó giá usare
[/nota]Segui, se sei interessato, le sguenti procedure:
-1- installa l´estensione
-2- finita l´installazione, clicca col tasto sx sulla estensione e poi lá dove ho cerchiato in rosso nell´immagine seguente (scusa ma io ormai uso e parlo tedesco ovunque, in italiano dovresti tramite l´immagine individuare la voce facilmente):
-3- ti verrá aperta una finestra come la seguente:
cancella tutto quello che vi é scritto nel riquadro bianco ed incolla il seguente codice (nel quale viene inglobato lo script citato prima)
// ==UserScript==
// @name New Userscript
// @namespace http://tampermonkey.net/
// @version 0.1
// @description try to take over the world!
// @author You
// @match http://*/*
// @grant none
// ==/UserScript==
(function() {
'use strict';
MathJax.Hub.Config({
extensions: ["tex2jax.js"],
jax: ["input/TeX","output/HTML-CSS"],
"HTML-CSS": {
styles: {".MathJax_Preview": {visibility: "hidden"}}
},
tex2jax: {inlineMath: [["$","$"],["\\(","\\)"]]},
TeX: {extensions: ["AMSmath.js","AMSsymbols.js","http://sonoisa.github.io/xyjax_ext/xypic.js"]}
// ^^^^^^^^load xypic.js
});
})(); e clicca su salva come visualizzato e cerchiato in nero nell´immagine seguente:adesso hai finito e se ricarichi la pagina di questa discussione dovresti visualizzare i digrammi (preciso che puó capitare che a primo uso non visualizza un tubo allora ricarica la pagina che dovrebbe andare
, che dire? Sempre meglio di niente o almeno per le frecce curve e alcune in diagonale poiché proprio per queste si usa questa estensione (http://meta.math.stackexchange.com/questions/14986/is-it-possible-to-draw-a-diagonal-arrow-in-a-commutative-diagram/14987#14987))Inoltre nella pagina di prima, ovvero questa, trovi tanti esempi dai quali puoi partire, alcuni sono fantastici come quello del metodo di Newton,... ad esempio:
http://sonoisa.github.io/xyjax/xyjax.ht ... rixFeature (il quinto diagramma é fantastico poterlo visualizzare online con tanto di codice LaTex e a colori anche)
http://sonoisa.github.io/xyjax/xyjax.ht ... on'sMethod
http://sonoisa.github.io/xyjax/xyjax.ht ... seFunction
per il tuo digramma postato dopo, se hai seguito i passi di sopra, si ha con uno stile migliore, poiché anche l´occhio vuole la sua parte, la seguente:
$$ \xymatrix{ &\pi_1(A) \ar[rd]^{i_{\ast}} \\\pi_1(A\cap B) \ar[ru]^{\alpha_{\ast}} \ar[rd]_{\beta_{ \ast}} &&\pi_1(A\cup B) \\&\pi_1(B) \ar[ru]_{j_{\ast}} } $$
Esiste la stessa estensione anche per Firefox, quella uso io é questa, sinceramente lavora meglio su Mozilla che su Chrome (ovviamente parlo per me e per le versioni di Chrome e Mozilla che ho ed uso), lo script é lo stesso e per aggiugerlo si seguono gli stessi identici passi di prima
ps.=volendo visualizzare questo diagramma:
\xymatrix{ & T(TM) & T^\ast(T^\ast M) \\ & T^\ast M \ar_{X_H} \ar[ur]_{\theta_H} \\ \mathbb R \ar@/^2pc/[uur]^{X_H\circ(\alpha\circ\phi)} \ar@/^1pc/[ur]^{\alpha\circ\gamma} \ar[r]^{\gamma} \ar@/_1pc/[dr]_{x\circ\gamma} \ar@/_2pc/[ddr]_{x_\iota\circ(x\circ\gamma)} & M \ar[d]_x \\ & TM \ar[d]_{X_\iota} \ar[dr]^{\theta_n} \\ & T(TM) & T^\ast(TM) } coi i delimitatori "tex" si ha:
[tex]\xymatrix{ & T(TM) & T^\ast(T^\ast M) \\ & T^\ast M \ar_{X_H} \ar[ur]_{\theta_H} \\ \mathbb R \ar@/^2pc/[uur]^{X_H\circ(\alpha\circ\phi)} \ar@/^1pc/[ur]^{\alpha\circ\gamma} \ar[r]^{\gamma} \ar@/_1pc/[dr]_{x\circ\gamma} \ar@/_2pc/[ddr]_{x_\iota\circ(x\circ\gamma)} & M \ar[d]_x \\ & TM \ar[d]_{X_\iota} \ar[dr]^{\theta_n} \\ & T(TM) & T^\ast(TM) }[/tex]
usando lo script l´aspetto migliora:
\(\xymatrix{ & T(TM) & T^\ast(T^\ast M) \\ & T^\ast M \ar_{X_H} \ar[ur]_{\theta_H} \\ \mathbb R \ar@/^2pc/[uur]^{X_H\circ(\alpha\circ\phi)} \ar@/^1pc/[ur]^{\alpha\circ\gamma} \ar[r]^{\gamma} \ar@/_1pc/[dr]_{x\circ\gamma} \ar@/_2pc/[ddr]_{x_\iota\circ(x\circ\gamma)} & M \ar[d]_x \\ & TM \ar[d]_{X_\iota} \ar[dr]^{\theta_n} \\ & T(TM) & T^\ast(TM) }\)
per chi non usa lo script puó vedere qui
oppure:
\xymatrix{ & & & C_1 \ar[rr]^{\gamma_1} \ar[dd]_(.6){f^\prime} & & C_2 \ar[dd]_(.6){g^\prime} \ar[rr]^{\gamma_2} & & C_3 \ar[rr] \ar[dd]_(.6){h^\prime} & & 0 \\ & & A_1 \ar[dd]^(.4)f \ar[ur]^{k_1} \ar[rr]^(.6){\alpha_1} & & A_2 \ar[ur]^{k_2} \ar[dd]^(.4)g \ar[rr]^(.6){\alpha_2} & & A_3 \ar[ur]^{k_3} \ar[dd]^(.4)h \ar[rr] & & 0 \\ & 0 \ar[rr] & & D_1 \ar[rr]^(.4){\delta_1} & & D_2 \ar[rr]^(.4){\delta_2} & & D_3 \\ 0 \ar[rr] & & B_1 \ar[rr]^{\beta_1} \ar[ur]^{j_1} & & B_2 \ar[ur]^{j_2} \ar[rr]^{\beta_2} & & B_3 \ar[ur]^{j_3} }[tex]\xymatrix{ & & & C_1 \ar[rr]^{\gamma_1} \ar[dd]_(.6){f^\prime} & & C_2 \ar[dd]_(.6){g^\prime} \ar[rr]^{\gamma_2} & & C_3 \ar[rr] \ar[dd]_(.6){h^\prime} & & 0 \\ & & A_1 \ar[dd]^(.4)f \ar[ur]^{k_1} \ar[rr]^(.6){\alpha_1} & & A_2 \ar[ur]^{k_2} \ar[dd]^(.4)g \ar[rr]^(.6){\alpha_2} & & A_3 \ar[ur]^{k_3} \ar[dd]^(.4)h \ar[rr] & & 0 \\ & 0 \ar[rr] & & D_1 \ar[rr]^(.4){\delta_1} & & D_2 \ar[rr]^(.4){\delta_2} & & D_3 \\ 0 \ar[rr] & & B_1 \ar[rr]^{\beta_1} \ar[ur]^{j_1} & & B_2 \ar[ur]^{j_2} \ar[rr]^{\beta_2} & & B_3 \ar[ur]^{j_3} }[/tex]
\[\xymatrix{ & & & C_1 \ar[rr]^{\gamma_1} \ar[dd]_(.6){f^\prime} & & C_2 \ar[dd]_(.6){g^\prime} \ar[rr]^{\gamma_2} & & C_3 \ar[rr] \ar[dd]_(.6){h^\prime} & & 0 \\ & & A_1 \ar[dd]^(.4)f \ar[ur]^{k_1} \ar[rr]^(.6){\alpha_1} & & A_2 \ar[ur]^{k_2} \ar[dd]^(.4)g \ar[rr]^(.6){\alpha_2} & & A_3 \ar[ur]^{k_3} \ar[dd]^(.4)h \ar[rr] & & 0 \\ & 0 \ar[rr] & & D_1 \ar[rr]^(.4){\delta_1} & & D_2 \ar[rr]^(.4){\delta_2} & & D_3 \\ 0 \ar[rr] & & B_1 \ar[rr]^{\beta_1} \ar[ur]^{j_1} & & B_2 \ar[ur]^{j_2} \ar[rr]^{\beta_2} & & B_3 \ar[ur]^{j_3} }\]
clic qui per chi non usa lo script
UPDATE:
ed anche:
\xymatrix@C=2cm{
& & H(Z) \ar@/^2.0pc/[rr]^{F(f^{op} \circ g^{op})} \ar[r]^{H^{*}(g^{op})}
& H(Y) \ar@{=}[dl] \ar[r]^{H^{*}(f^{op})}
& H(X) \ar@{=}[dl] \ar@/^2.0pc/@{=>}[ddll] \\
& H(Z) \ar@{=}[ur]
& H(Y) \ar_{G(g^{op})}
& H(X) \ar@{=}[dl] \ar_{G(f^{op})} \\
H(Z) \ar[r]_{H^{*}(g^{op})} \ar@{=}[ur]
& H(Y) \ar@{=}[ur] \ar[r]_{H^{*}(f^{op})} \ar_{G(g^{op})}
& H(X) \ar_{G(f^{op})}
\ar@/^2.0pc/[uu]^{G(f^{op} \circ g^{op})}
}questo non riesco proprio a visualizzarlo senza estensione, ergo uso lo script direttamente:
\[
\xymatrix@C=2cm{
& & H(Z) \ar@/^2.0pc/[rr]^{F(f^{op} \circ g^{op})} \ar[r]^{H^{*}(g^{op})}
& H(Y) \ar@{=}[dl] \ar[r]^{H^{*}(f^{op})}
& H(X) \ar@{=}[dl] \ar@/^2.0pc/@{=>}[ddll] \\
& H(Z) \ar@{=}[ur]
& H(Y) \ar_{G(g^{op})}
& H(X) \ar@{=}[dl] \ar_{G(f^{op})} \\
H(Z) \ar[r]_{H^{*}(g^{op})} \ar@{=}[ur]
& H(Y) \ar@{=}[ur] \ar[r]_{H^{*}(f^{op})} \ar_{G(g^{op})}
& H(X) \ar_{G(f^{op})}
\ar@/^2.0pc/[uu]^{G(f^{op} \circ g^{op})}
}
\]
questi sono semplicissimi:
\xymatrix{
A \ruppertwocell^f{\alpha}
\rlowertwocell_h{\beta}
\ar[r]|{g}
&B\\
}
\xymatrix{
& A \ar[d]^{i} \ar@{-->}[dl]_-{\exists \tilde{\varphi}} \\
B \ar[r]^{\varphi} &C
}
anche qui uso l´estensione:
\[\xymatrix{
A \ruppertwocell^f{\alpha}
\rlowertwocell_h{\beta}
\ar[r]|{g}
&B\\
} \]\[
\xymatrix{
& A \ar[d]^{i} \ar@{-->}[dl]_-{\exists \tilde{\varphi}} \\
B \ar[r]^{\varphi} &C
}
\]
qualcosa di anomalo come:
\xymatrix{A \ar@(dr,dl)[r]\ar@(dr,dl)[rr]
&B\ar@(d,r)[dl] &C \\
E \ar@(ul,ur)}con lo script si ha:
\[\xymatrix{A \ar@(dr,dl)[r]\ar@(dr,dl)[rr]
&B\ar@(d,r)[dl] &C \\
E \ar@(ul,ur)} \]
per chi non usa lo script puó vedere qui
ps= lo script va in conflitto alle volte con la codifica Ascimathml usata da alcuni utenti, ergo visualizzo male le loro formule...
[tex]\xymatrix{
&\pi_1(A) \ar[rd]^{i_{\ast}} \\\pi_1(A\cap B) \ar[ru]^{\alpha_{\ast}} \ar[rd]_{\beta_{ \ast}} &&\pi_1(A\cup B) \\&\pi_1(B) \ar[ru]_{j_{\ast}} }[/tex]
&\pi_1(A) \ar[rd]^{i_{\ast}} \\\pi_1(A\cap B) \ar[ru]^{\alpha_{\ast}} \ar[rd]_{\beta_{ \ast}} &&\pi_1(A\cup B) \\&\pi_1(B) \ar[ru]_{j_{\ast}} }[/tex]
"dan95":
È un bel problema, anche con diagrammi semplici come A \ar[r] B dà errore
Ciao, ora dovrebbe funzionare di nuovo. Oltre a Xy-pic (in realtà il pacchetto xymatrix), per alcuni tipi di diagrammi si può usare anche AMScd, con i soliti delimitatori di MathJaX, tramite il comando
\require{AMScd}.Esempio:
\require{AMScd}
\begin{CD}
A @>a>> B\\
@VVbV @VVcV\\
C @>d>> D
\end{CD}\(\require{AMScd}
\begin{CD}
A @>a>> B\\
@VVbV @VVcV\\
C @>d>> D
\end{CD}\)
[xdom="Raptorista"]Sposto in Questioni tecniche.[/xdom]
Posso chiederti di spostarlo nella sezione tecnica del forum.
È un bel problema, anche con diagrammi semplici come A \ar[r] B dà errore
Grazie TeM
Sul mio editor ho usato il pacchetto xy e funziona, qui stessa sintassi non funziona.
Sul mio editor ho usato il pacchetto xy e funziona, qui stessa sintassi non funziona.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo