Applicazione della seconda legge di Newton

[Cry.A]

la figura seguente rappresenta un corpo soggetto a tre forze. nella scala del disegno, un vettore forza di 1 mm corrisponde a una forza di valore 1 N. la massa del corpo è di 2,1 kg. questa è l'immagine del disegno del libro. ogni vettore è di due centimetri

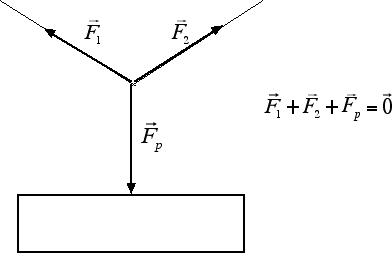
calcola l'accelerazione con cui si muove il corpo.
qualcuno potrebbe spiegarmi bene i passaggi e le formule giuste perchè io ho usato la regola del parallelogramma e il teorema di pittagore ma non so se è giusto usarlo in questo caso... (avevo già fatto una domanda simile a questa ma per sbaglio ho cliccato miglior risposta e quindi non ho potuto rispondere e chiedere nient'altro )grazie mille in anticipo

Aggiunto 1 minuto più tardi:

e da contare solo la figura delle 3 forze ...il rettangolo e f1+f2+fp=0 no

[ce8c0e31f941cc14ed8def9a9c5c3a60a8400d85]

Supponendo che l'angolo tra le prime due forze sia retto, la loro risultante
non è altro che la diagonale del quadrato che vanno a delineare, opposta
alla forza peso. Per tal motivo, considerando convenzionalmente come
positive le forze verso l'alto, l'intensità totale della forza che risente il cor-
po è pari a

[math]\sum F_i = \sqrt{2}\,F_1 - F_p = \sqrt{2}\cdot 20 - 2.1\cdot 9.81 \approx 7.68\,N\\[/math]

.

Per il calcolo del modulo dell'accelerazione non rimane che applicare la
seconda legge di Newton, secondo la quale:

[math]\sum F_i = m\,a[/math]

. Nello spe-
cifico, si ottiene

[math]a \approx \frac{7.68}{2.1} \approx 3.66\frac{m}{s^2}[/math]

. ;)