Il calendario Impossibile, un anno dopo

[Al-Mat]

Salve a tutti;
Ripubblico un dilemma che ormai mi perseguita da diversi anni, l'anno scorso non ebbi esito positivo, anche perché forse spiegai in maniera difficile il problema. Questa volta cerco di essere più chiaro.
Il problema è il seguente:
Ci sono 12 squadre: (A, B, C, D,....., L)
Le 12 squadre devono affrontarsi in un girone all'italiana di sola andata (quindi 11 giornate)
Ogni giornata di campionato è composto da 3 fasce orarie in cui giocare (15:00, 18:00, 21:00), ad ogni fascia oraria si disputano 2 partite.
DOMANDA
E' possibile la creazione di un calendario in cui, oltre allo scontro diretto, ogni squadra gioca esattamente per 2 volte nella stessa fascia oraria con tutte le altre squadre?
Esempio per essere più chiaro
Giornata 1
Ore 15:00
A - B; C - D;
Ore 18:00
E - F; G - H;
Ore 21:00
I - J; K - L.

In questo esempio la squadra A gioca contro B (e non la deve più affrontare in campionato) e gioca nella stessa fascia oraria con C e D, quindi con queste ultime 2 squadre può giocarci soltanto un'altra volta nella stessa fascia oraria (escluso lo scontro diretto).
Credo di essere stato chiaro ed esaustivo e spero di incontrare qualche buon anima che risolva una volta per tutte questo problema (o al limite mi dimostra la sua infattibilità).

[moccidentale]

.

[axpgn]

"sellacollesella":Ovviamente, tutto ciò al netto di una eventuale dimostrazione teorica che metta una parola fine a tutto!

Che è quello che vorrebbe fare ogni buon matematico

[axpgn]

"sellacollesella":Anche questa sarebbe una bella idea, ma ... tocca pensarci ... ora come ora non saprei.

Provo a buttare lì un inizio ...

Le partite sono $66$, a ciascuna va assegnata una giornata e una fascia (es. cf: 07-2)
Si inizia mettendo $ab, ac, ..., al$ sempre nella prima fascia di ogni giornata, poi si prosegue con $bc, bd, ...$ ecc.
Se si riesce a piazzarle tutte e $66$ ...
Non so quanto possa essere lunga 'sta cosa

[axpgn]

La prima fascia è sistemata, adesso bisogna costruire le altre ...

[axpgn]

Lo schema che ho usato non è replicabile per le altre due fasce quindi sono al punto di partenza ...

[moccidentale]

.

[utente__medio11]

"sellacollesella":Ok, allora pian pianino un po' di nebbia si sta diradando e cominciamo ad avere dei punti d'incontro, confermando quanto aveva già intuito utente_medio (porta pazienza, ma io e l'intuito mai incontrati).

Figurati!

Comunque ho scritto un programmino che dovrebbe testare tutte le $90^11$ possibili combinazioni di fasce orarie:

#include <iostream>
#include <algorithm>

using namespace std;

const unsigned int N = 12;
const unsigned int U[6] = {0, 0, 1, 1, 2, 2};
const unsigned int V[6] = {0, 1, 2, 3, 4, 5};

void definisci_squadre(char s[N])
{
    for(unsigned int i = 0; i < N; ++i)
    {
        s[i] = 'A' + i;
    }
}

void definisci_giornate(unsigned int g[N - 1][N / 2][2])
{
    unsigned int u[N] = {N - 1};
    for(unsigned int i = 0, j; i < N - 1; ++i)
    {
        for(j = 2, u[1] = i; j < N; u[j] = (u[j - 1] + 1) % (N - 1), ++j);
        for(unsigned int j = 0; j < N / 2; ++j)
        {
            g[i][j][0] = u[j + 1];
            g[i][j][1] = u[(N - j) % N];
        }
    }
}

void stampa_calendario(const unsigned int g[N - 1][N / 2][2], const unsigned int f[N - 1][2][N / 2], const char s[N])
{
    for(unsigned int i = 0; i < N - 1; ++i)
    {
        cout << "\n GIORNATA " << i + 1 << ":\t";
        for(unsigned int j = 0; j < N / 2; ++j)
        {
            const unsigned int (&r)[2] = g[i][f[i][1][j]];
            cout << s[r[0]] << "-" << s[r[1]] << (j % 2 && j != N / 2 - 1 ? " | " : "  ");
        }
    }
    cout << "\n";
}

void inizializza_fasce_orarie(unsigned int f[N - 1][2][N / 2])
{
    for(unsigned int i = 0; i < N - 1; ++i)
    {
        copy(U, U + N / 2, f[i][0]);
        copy(V, V + N / 2, f[i][1]);
    }
}

bool testa_fasce_orarie(const unsigned int g[N - 1][N / 2][2], const unsigned int f[N - 1][2][N / 2])
{
    unsigned int v[N][N] = {};
    for(unsigned int i = 0; i < N - 1; ++i)
    {
        for(unsigned int j = 0; j < N / 2; j += 2)
        {
            const unsigned int (&r1)[2] = g[i][f[i][1][j]];
            const unsigned int (&r2)[2] = g[i][f[i][1][j + 1]];
            if((r1[0] < r2[0] ? ++v[r2[0]][r1[0]] : ++v[r1[0]][r2[0]]) == 3 ||
               (r1[0] < r2[1] ? ++v[r2[1]][r1[0]] : ++v[r1[0]][r2[1]]) == 3 ||
               (r1[1] < r2[0] ? ++v[r2[0]][r1[1]] : ++v[r1[1]][r2[0]]) == 3 ||
               (r1[1] < r2[1] ? ++v[r2[1]][r1[1]] : ++v[r1[1]][r2[1]]) == 3)
            {
                return false;
            }
        }
    }
    return true;
}

bool ripartizione_successiva(unsigned int u[N / 2], unsigned int v[N / 2])
{
    unsigned int i = N / 2;
    while(--i && u[i - 1] >= u[i]);
    if(i)
    {
        reverse(u + i, u + N / 2);
        for(unsigned int j = i; j < N / 2; ++j)
        {
            if(u[i - 1] < u[j])
            {
                swap(u[i - 1], u[j]);
                for(unsigned int w[3] = {0, 2, 4}, k = 0; k < N / 2; ++k)
                {
                    v[w[u[k]]++] = k;
                }
                return true;
            }
        }
    }
    copy(U, U + N / 2, u);
    copy(V, V + N / 2, v);
    return false;
}

int main()
{
    char s[N]; //squadre
    definisci_squadre(s);

    unsigned int g[N - 1][N / 2][2]; //giornate
    definisci_giornate(g);

    unsigned int f[N - 1][2][N / 2]; //fasce orarie
    inizializza_fasce_orarie(f);

    do
    {
        if(testa_fasce_orarie(g, f))
        {
            stampa_calendario(g, f, s);
            break;
        }
    }
    while(ripartizione_successiva(f[0][0], f[0][1]) || ripartizione_successiva(f[1][0], f[1][1]) ||
          ripartizione_successiva(f[2][0], f[2][1]) || ripartizione_successiva(f[3][0], f[3][1]) ||
          ripartizione_successiva(f[4][0], f[4][1]) || ripartizione_successiva(f[5][0], f[5][1]) ||
          ripartizione_successiva(f[6][0], f[6][1]) || ripartizione_successiva(f[7][0], f[7][1]) ||
          ripartizione_successiva(f[8][0], f[8][1]) || ripartizione_successiva(f[9][0], f[9][1]) ||
          ripartizione_successiva(f[10][0], f[10][1]));
}

L'ho scritto tanto per, ma devo ammettere che quando l'ho lanciato un po' ci ho sperato che ne uscisse subito fuori qualcosa!
Poi chissà, magari qualcuno del forum si trova per le mani un computer quantistico!

Scherzi a parte, mi sa che l'unica strada è quella di riflettere ulteriormente sul problema, se non per giungere ad una dimostrazione teorica definitiva, quantomeno per fissare qualche vincolo allo scopo di abbassare notevolmente il muro dei $90^11$.


P.S.
Qualcuno ha provato a chiedere a qualche AI?

[moccidentale]

.

[axpgn]

Fantastico

Ma sta ancora lavorando? Vedo un numerino che gira ...

[moccidentale]

.

[utente__medio11]

"sellacollesella":Scherzi a parte, credi che sarà mai possibile averne uno tra le mani in tempi umani?

Mi dispiace, ma non sono ferrato, né molto informato, sull'argomento.

"sellacollesella":D'altro canto, come sopra aggiornato, tramite il "metodo ignorante" ho ottenuto un calendario da \( 80 \).

Poi, visto che ogni tanto anch'io ho qualche sprazzo di lucidità, mi sono chiesto se non fosse un tantino stupido continuare ad insistere a generare calendari completamente a random, bensì non fosse un po' più intelligente partire dal miglior calendario e apportare piccole modifiche a random che, qualora lo migliori, comporterebbero essere il nuovo miglior calendario (che assomiglia all'idea di axpgn di "costruirlo").

Così, in appena un migliaio di iterazioni, da \( 80 \) sono passato a \( \color{red}{\boxed{52\,}} \), il che mi ha fatto sobbalzare dalla sedia, pensando di avere la situazione in mano ... ma niente, poi non sono più riuscito a scendere ulteriormente!

L'idea era buona, peccato che il "countdown" si sia bloccato...

"sellacollesella":Ah quel numerino girerà per l'eternità essendo una gif registrata ieri notte.

[axpgn]

"sellacollesella": Qualora non dovessi più intervenire, significa che il computer si è fuso, amen.

In tal caso proporrei una colletta

[utente__medio11]

Per chi volesse fare qualche tentativo, ho scritto un programmino che permette di interagire semplicemente col problema scambiando due partite di una stessa giornata:

#include <iostream>
#include <algorithm>

using namespace std;

const unsigned int N = 12;
const unsigned int V[6] = {0, 1, 2, 3, 4, 5};

void definisci_squadre(char s[N])
{
    for(unsigned int i = 0; i < N; ++i)
    {
        s[i] = 'A' + i;
    }
}

void definisci_giornate(unsigned int g[N - 1][N / 2][2])
{
    unsigned int u[N] = {N - 1};
    for(unsigned int i = 0, j; i < N - 1; ++i)
    {
        for(j = 2, u[1] = i; j < N; u[j] = (u[j - 1] + 1) % (N - 1), ++j);
        for(unsigned int j = 0; j < N / 2; ++j)
        {
            g[i][j][0] = u[j + 1];
            g[i][j][1] = u[(N - j) % N];
        }
    }
}

void stampa_calendario(const unsigned int g[N - 1][N / 2][2], const unsigned int f[N - 1][N / 2], const char s[N])
{
    cout << "\n\t\t\t    PARTITA\n\t        ------------------------------\n\t\t ";
    for(unsigned int i = 0; i < N / 2; cout << i++ + 1 << (i % 2 ? "    " : "     "));
    cout << "\n";
    for(unsigned int i = 0; i < N - 1; ++i)
    {
        cout << "\n GIORNATA " << i + 1 << ":\t";
        for(unsigned int j = 0; j < N / 2; ++j)
        {
            const unsigned int (&r)[2] = g[i][f[i][j]];
            cout << s[r[0]] << "-" << s[r[1]] << (j % 2 && j != N / 2 - 1 ? " | " : "  ");
        }
    }
    cout << "\n";
}

void inizializza_fasce_orarie(unsigned int f[N - 1][N / 2])
{
    for(unsigned int i = 0; i < N - 1; copy(V, V + N / 2, f[i++]));
}

void stampa_test_fasce_orarie(const unsigned int g[N - 1][N / 2][2], const unsigned int f[N - 1][N / 2], const char s[N])
{
    unsigned int v[N][N] = {};
    for(unsigned int i = 0; i < N - 1; ++i)
    {
        for(unsigned int j = 0; j < N / 2; j += 2)
        {
            const unsigned int (&r1)[2] = g[i][f[i][j]];
            const unsigned int (&r2)[2] = g[i][f[i][j + 1]];
            r1[0] < r2[0] ? ++v[r2[0]][r1[0]] : ++v[r1[0]][r2[0]];
            r1[0] < r2[1] ? ++v[r2[1]][r1[0]] : ++v[r1[0]][r2[1]];
            r1[1] < r2[0] ? ++v[r2[0]][r1[1]] : ++v[r1[1]][r2[0]];
            r1[1] < r2[1] ? ++v[r2[1]][r1[1]] : ++v[r1[1]][r2[1]];
        }
    }
    cout << "\n\n";
    unsigned int cont = 0;
    for(unsigned int i = 1; i < N; ++i)
    {
        cout << "\n " << s[i] << "  ";
        for(unsigned int j = 0; j < i; ++j)
        {
            cont += v[i][j] < 2 ? 2 - v[i][j] : v[i][j] - 2;
            cout << v[i][j] << " ";
        }
    }
    cout << "\n\n    ";
    for(unsigned int i = 0; i < N - 1; cout << s[i++] << " ");
    cout << "\tDISTANZA = " << cont << "\n\n";
}


int main()
{
    char s[N]; //squadre
    definisci_squadre(s);

    unsigned int g[N - 1][N / 2][2]; //giornate
    definisci_giornate(g);

    unsigned int f[N - 1][N / 2]; //fasce orarie
    inizializza_fasce_orarie(f);

    for(unsigned int g_ = 1, p1 = 1, p2 = 1; g_ < N;)
    {
        system("cls");
        swap(f[g_ - 1][p1 - 1], f[g_ - 1][p2 - 1]);
        stampa_calendario(g, f, s);
        stampa_test_fasce_orarie(g, f, s);
        cout << "\n SCAMBIA PARTITE:\n\n GIORNATA -> ";
        cin >> g_;
        cout << " PARTITA 1 -> ";
        cin >> p1;
        cout << " PARTITA 2 -> ";
        cin >> p2;
    }
}

[moccidentale]

.

[utente__medio11]

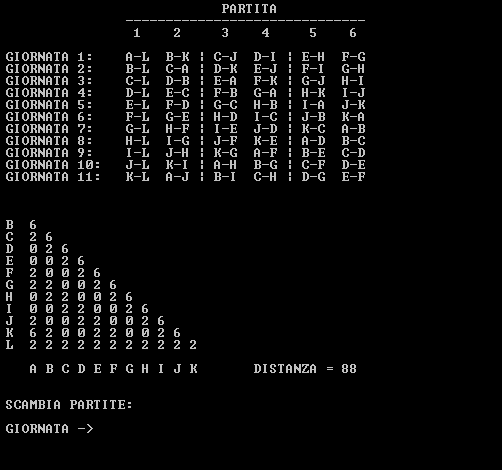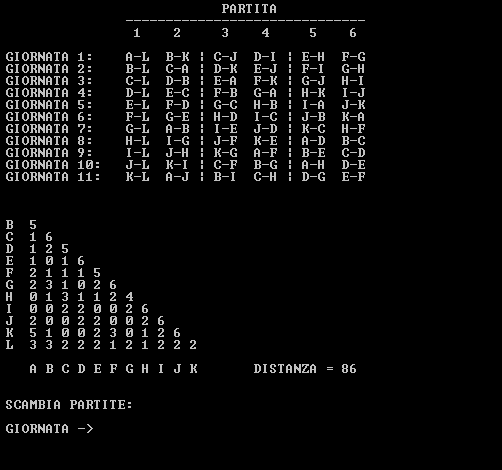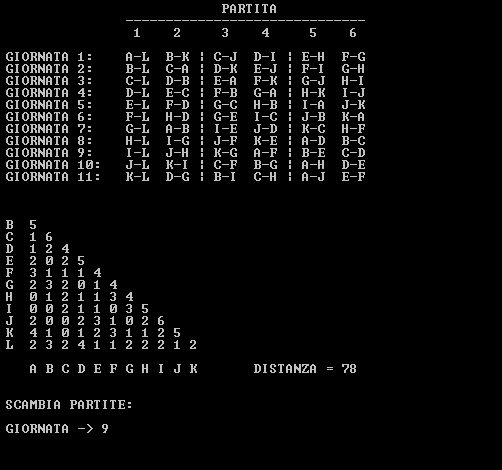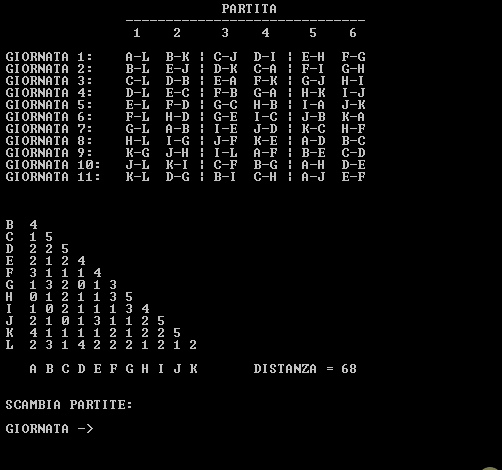
"sellacollesella":@utente_medio: bello! È grosso modo una delle mie ultime strategie messe in atto, anche se randomizzate.

Giocando un po' con gli scambi sono arrivato anche io ad una distanza di $26$, oltre la quale non riesco a scendere... chissà?!

"sellacollesella":Tuttavia, vista la situazione di stallo, almeno a me appare così, credo sia il momento di cambiare; ma cosa? Secondo me, una possibilità è ricondursi ad un modello di programmazione non lineare, intera e binaria...

...non sembra riuscire a dare una risposta; 'sto fetente!

[moccidentale]

.

[utente__medio11]

A questo punto anche a me viene da pensare che la risposta sia già nel titolo del topic!
In ogni caso dal punto di vista della programmazione non saprei più cosa tentare; alla fine, a prescindere da come lo poni, il problema sembra computazionalmente proibitivo.
Al massimo, se capita, proverò a rifletterci ancora un po' al fine di trovare una dimostrazione teorica.

[axpgn]

Computazionalmente si potrebbe provare un problema più piccolo: 8 squadre, 2 fasce, 1 sola volta in contemporanea.

[moccidentale]

.

[utente__medio11]

"axpgn":Computazionalmente si potrebbe provare un problema più piccolo: 8 squadre, 2 fasce, 1 sola volta in contemporanea.

Non dovrebbe essere sempre massimo $2$ volte in contemporanea (escluso lo scontro diretto)?
Detto ciò, ho adattato il codice qui postato per testare i $6^7$ possibili calendari (in termini di fasce orarie), e ottengo che nessuno di essi soddisfa i vincoli imposti. Confermo inoltre che la distanza minima è pari a $28$.

Quindi, a meno di errori nel codice, possiamo concludere che con $8$ squadre il problema non ha soluzioni. Questo però non ci aiuta più di tanto col caso di $12$ squadre di nostro interesse.